こんにちは。相城です。今回は扇形の面積や弧の長さのところでよく出題される図形の瞬殺技をご紹介します。
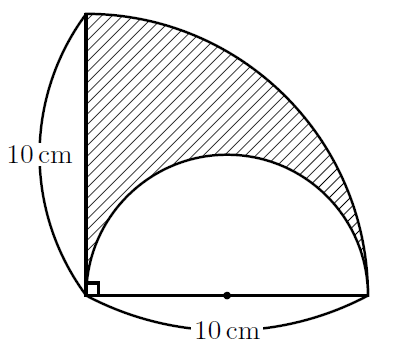
下の図の斜線部分の面積を求めなさい。また、斜線部分の周りの長さを求めなさい。ただし、円周率は![]() とします。
とします。
よく中学校1年生で登場する図形問題である。ただこの図形は少し奥が深いのです。
意外と知らない人が多いので紹介しておきます。あまり参考書にも載ってなかったりするので, 個人的にはお気に入りの公式なんですけどね。
先に瞬殺技を使って答えを出すと, この図形の斜線部分の面積は![]() cm
cm![]() で斜線部分の周りの長さは
で斜線部分の周りの長さは![]() (cm)なんです。
(cm)なんです。
そのからくりを言うと, 上の図形で中心角が90![]() の扇形の半径が
の扇形の半径が![]() cmなら斜線部分の面積は
cmなら斜線部分の面積は![]() cm
cm![]() であるし, 斜線部分の周りの長さは
であるし, 斜線部分の周りの長さは![]() cmになります。
cmになります。
以下それを証明します。
【証明】
半径![]() cm,中心角90
cm,中心角90![]() の扇形と半径
の扇形と半径![]() cmで中心角180
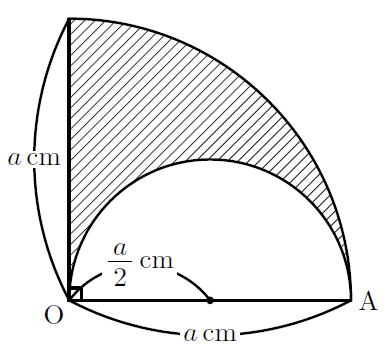
cmで中心角180![]() の扇形が図のように線分OAでぴったり重なっていることを考える。このとき斜線部分の面積は次のように与えられる。
の扇形が図のように線分OAでぴったり重なっていることを考える。このとき斜線部分の面積は次のように与えられる。![]() の扇形・半径
の扇形・半径![]() 半円・半径
半円・半径![]()
![]()
![]()
![]()
ここで半径![]() cm,中心角180
cm,中心角180![]() の扇形の面積は,
の扇形の面積は,![]()
![]()
![]() より, 斜線部分の面積は, 斜線部分ではない扇形の面積と同じであることがわかる。したがって, 斜線部分の面積を求めたければ, 斜線部分でない部分の面積を求めるとよい。
より, 斜線部分の面積は, 斜線部分ではない扇形の面積と同じであることがわかる。したがって, 斜線部分の面積を求めたければ, 斜線部分でない部分の面積を求めるとよい。
このことから, (斜線部分の面積)![]()
という公式が得られる。
次に周りの長さについての証明をします。
半径![]() cm,中心角90
cm,中心角90![]() の弧の長さを求めると,
の弧の長さを求めると, ![]()
半径![]() cm, 中心角180
cm, 中心角180![]() の弧の長さを求めると,
の弧の長さを求めると,![]()
となり、周りの長さは次式で考えられる。
(周りの長さ)![]()
![]()
よって,
(周りの長さ)![]() (cm)という公式が得られる。
(cm)という公式が得られる。
 数樂管理人のブログ
数樂管理人のブログ