こんにちは。今回は2直線のなす角をベクトルを用いて求めてみましょう。
【例題】2直線![]() ,
, ![]() のなす角
のなす角![]() を求めよ。ただし,
を求めよ。ただし, ![]() は鋭角とする。
は鋭角とする。
【解法①:方向ベクトルを用いる場合】先ずは与式を![]() について解き, グラフを描いて様子を見る。
について解き, グラフを描いて様子を見る。
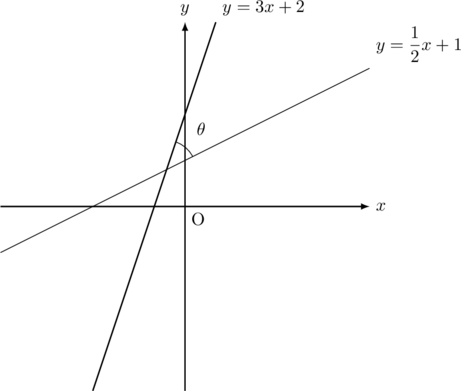
2つのグラフは
内積の公式より,
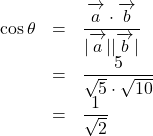
より,
【解法②:法線ベクトルを用いる場合】
2直線
また,
内積の公式より,
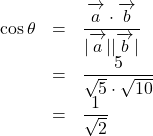
より,
こんな感じで求めていきます。
こんにちは。今回は2直線のなす角をベクトルを用いて求めてみましょう。
【例題】2直線![]() ,
, ![]() のなす角
のなす角![]() を求めよ。ただし,
を求めよ。ただし, ![]() は鋭角とする。
は鋭角とする。
【解法①:方向ベクトルを用いる場合】先ずは与式を![]() について解き, グラフを描いて様子を見る。
について解き, グラフを描いて様子を見る。

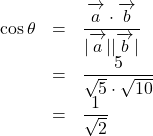
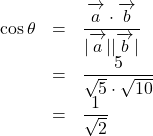
こんな感じで求めていきます。