TikZ：中学数学：√a+√b≠√a+bの理由

こんにちは。今回は $\sqrt{\mathstrut a}+\sqrt{\mathstrut b}\neq\sqrt{\mathstrut a+b}$ となる理由を書いておきます。

√5＋√3＝√8ではない

まず, 代数的に見ていきましょう。
$\sqrt{\mathstrut a}+\sqrt{\mathstrut b}=\sqrt{\mathstrut a+b}$ が成り立つなら,
両辺2乗しても成り立つので, 両辺を2乗すると,
左辺 $=\left(\sqrt{\mathstrut a}+\sqrt{\mathstrut b}\right)^2$
$=a+b+2\sqrt{ab}\cdots\textcircled{\scriptsize 1}$
右辺 $=\left(\sqrt{a+b}\right)^2$
$=a+b\cdots\textcircled{\scriptsize 2}$
このとき, $\textcircled{\scriptsize 1}\neq\textcircled{\scriptsize 2}$
よって, $\sqrt{\mathstrut a}+\sqrt{\mathstrut b}=\sqrt{\mathstrut a+b}$ とはならない。
つまり, $\sqrt5+\sqrt3=\sqrt8$ ではない。

幾何的に $\sqrt5+\sqrt3=\sqrt8$ とはならないことを見てみましょう。
下図のように, 面積が5cm $^2$ の正方形ABCDと面積が3cm $^2$ の正方形PCEFがくっついて並んでいる。このとき, BEを1辺とする正方形HBEGの面積を考える。

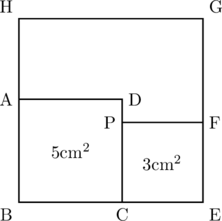
正方形ABCDの1辺は $\sqrt5$ cmで, 正方形PCEFの1辺は $\sqrt3$ cmになるので, 正方形HBEGの1辺は $\sqrt5+\sqrt3$ (cm)になる。仮に $\sqrt5+\sqrt3=\sqrt8$ が成り立つとすると, 正方形HBEGの面積は $\sqrt8\times\sqrt8=8$ cm $^2$ となるが, すでに, 正方形ABCDと正方形PCEFで面積は8cm $^2$ になっており, これはあり得ない。このことからも, $\sqrt5+\sqrt3=\sqrt8$ とはならないことがわかる。
したがって, $\sqrt5+\sqrt3=\sqrt8$ としてはいけない。

√5＋√3＝√8ではない

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル