こんにちは。はじめ見たときは度数法と勘違いしましたが, 度数法ではないのでお気を付けください。
グラフを描いて考えるといい
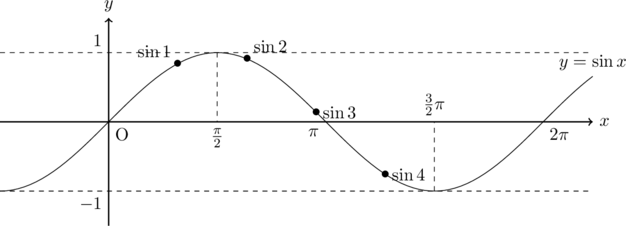
グラフより,
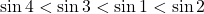
正確なグラフがなくとも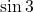 と
と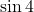 の大小は比較できると思います。ただ, 手書きでは正確なグラフが書きにくいので,
の大小は比較できると思います。ただ, 手書きでは正確なグラフが書きにくいので, 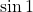 と
と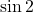 の大小比較では, グラフの軸を
の大小比較では, グラフの軸を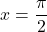 とした対称性から, その軸から離れている方が小さい値を取るというように手順を踏んで考える。このとき,
とした対称性から, その軸から離れている方が小さい値を取るというように手順を踏んで考える。このとき, 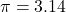 とすると, 軸は
とすると, 軸は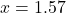 になり, 1と2では1の方が少し離れていることになるので,
になり, 1と2では1の方が少し離れていることになるので, 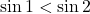 となります。したがって,
となります。したがって, 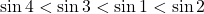 という結果を得ます。
という結果を得ます。同じように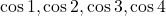 の大小関係も考えてみましょう。
の大小関係も考えてみましょう。
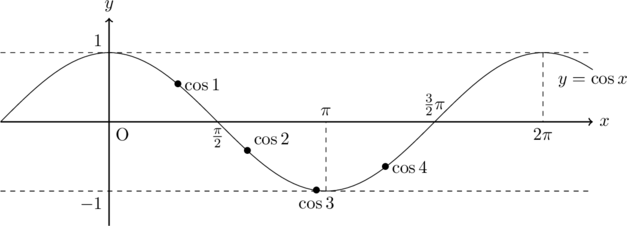
グラフより,
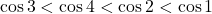
正確なグラフがなくとも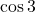 と
と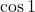 の大小は比較できると思います。ただ, 手書きでは正確なグラフが書きにくいので,
の大小は比較できると思います。ただ, 手書きでは正確なグラフが書きにくいので, 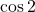 と
と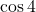 の大小比較では, グラフの軸を
の大小比較では, グラフの軸を とした対称性から, その軸から離れている方が大きい値を取るというように手順を踏んで考える。このとき,
とした対称性から, その軸から離れている方が大きい値を取るというように手順を踏んで考える。このとき, 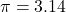 とすると, 軸は
とすると, 軸は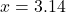 になり, 2と4では2の方が少し離れていることになるので,
になり, 2と4では2の方が少し離れていることになるので, 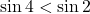 となります。したがって,
となります。したがって, 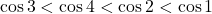 という結果を得ます。
という結果を得ます。

![]() の大小関係も考えてみましょう。
の大小関係も考えてみましょう。

![]() の大小関係も考えてみましょう。
の大小関係も考えてみましょう。