こんにちは。今回はタイトル通り, 連立方程式の解は一次関数の交点と同じになるということを示していきましょう。例題を解きながら見ていきます。
例:次の連立方程式を解きなさい。
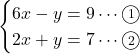
加減法で解くと, 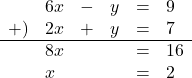
![]() を
を![]() に代入して,
に代入して, ![]() ,
, ![]()
![]()
ここで![]() ,
, ![]() を
を![]() について解くと,
について解くと, ![]() より,
より, ![]()
![]() より,
より, ![]()
これをグラフに書くと下図のようになり,
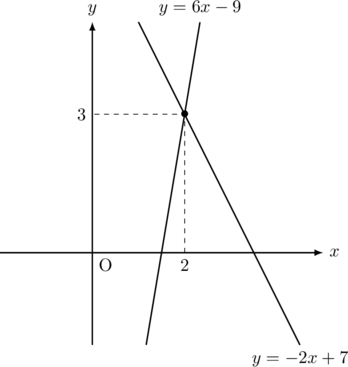
交点の座標は
このことから, 連立方程式
理由は, 連立方程式の解も一次関数の交点も, 2つの式を同時に満たす
それではまた。
こんにちは。今回はタイトル通り, 連立方程式の解は一次関数の交点と同じになるということを示していきましょう。例題を解きながら見ていきます。
例:次の連立方程式を解きなさい。
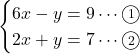
加減法で解くと, 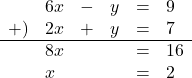
![]() を
を![]() に代入して,
に代入して, ![]() ,
, ![]()
![]()
ここで![]() ,
, ![]() を
を![]() について解くと,
について解くと, ![]() より,
より, ![]()
![]() より,
より, ![]()
これをグラフに書くと下図のようになり,
