こんにちは。今回は相関係数について書いておきます。先ずは公式を見てから, 例題を解いていきましょう。
相関係数rを求める公式
相関係数は2つの変量![]() のデータにおいて, 2つの関係(相関)の正負や強弱を調べるために設けられた値です。
のデータにおいて, 2つの関係(相関)の正負や強弱を調べるために設けられた値です。
一般に相関係数は次の式で与えられます。![]()
![]() は共分散,
は共分散, ![]() は変量
は変量![]() の標準偏差,
の標準偏差, ![]() は変量
は変量![]() の標準偏差
の標準偏差
変量![]() の平均をそれぞれ
の平均をそれぞれ![]() とし,データの総数を
とし,データの総数を![]() 個とすると,
個とすると, ![]()
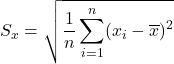
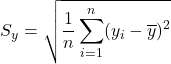
これらを![]() に代入すると,
に代入すると, 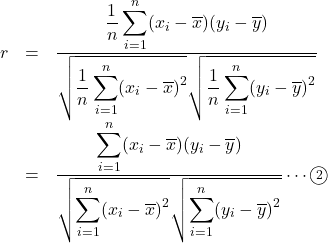
となり, ![]() が省かれた形で相関係数が求められる。
が省かれた形で相関係数が求められる。![]() の分母のルートをまとめると,
の分母のルートをまとめると, 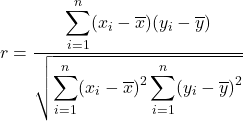
具体例を見ていきましょう
次の2つの変量![]() からなるA~Eの5つのデータがある。2つの変量
からなるA~Eの5つのデータがある。2つの変量![]() にはどのような相関があるか調べよ。
にはどのような相関があるか調べよ。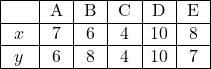
![]()
![]()
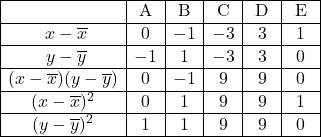
先の公式の確認
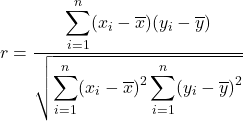
分子の和は表中の![]() の和なので
の和なので
分子![]()
分母は表中の![]() の和と
の和と![]() の和の積のルートなので,
の和の積のルートなので,
分母![]()
よって相関係数![]() は
は![]()
したがって2つの変量![]() には強い正の相関があることがわかる。
には強い正の相関があることがわかる。
相関係数
相関係数
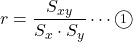
 の詳細。
の詳細。
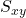 は共分散,
は共分散, 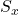 は変量
は変量 の標準偏差,
の標準偏差, 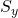 は変量
は変量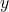 の標準偏差
の標準偏差
変量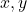 の平均をそれぞれ
の平均をそれぞれ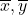 とし,データの総数を
とし,データの総数を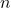 個とすると,
個とすると,
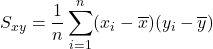
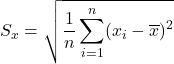
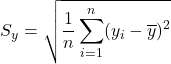
または,
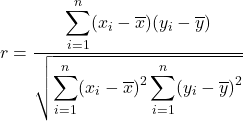
変量
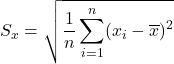
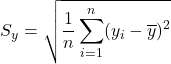
または,
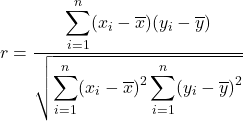
相関係数による強弱の度合い
相関係数の強弱の目安は, 感覚的に差があるかもしれないけど, 0.2ぐらいから下の値なら相関はほとんどなく, 0.2から0.4ぐらいが弱い相関, 0.4から0.7ぐらいまでが中程度の相関がある, 0.7から1ぐらいが強い相関があるという判断かなと思っています。また, 仮に相関係数が1なら, 散布図ではデータは右上がりの一直線上に並びます。 相関係数が![]() なら, 散布図ではデータは右下がりの一直線上に並びます。
なら, 散布図ではデータは右下がりの一直線上に並びます。
 数樂管理人のブログ
数樂管理人のブログ 

