こんにちは。今回は複素数の問題で式変形の例を見ていきます。例題を解きながら見ていきます。
複素数の問題の式変形の例①
【例】![]() ,
, ![]() は, 等式
は, 等式![]() を満たす0でない複素数とする。以下の問いに答よ。
を満たす0でない複素数とする。以下の問いに答よ。
(1) 複素数![]() を極形式で表せ。
を極形式で表せ。
(2) 複素数平面上で複素数0, ![]() ,
, ![]() を表す点をそれぞれO, A, Bとするとき,
を表す点をそれぞれO, A, Bとするとき, ![]() および
および![]() を求めよ。
を求めよ。
【解法】次の式変形は有名なので覚えておいてほしい。
両辺を![]() で割ると,
で割ると, ![]()
![]()
![]() の二次方程式として, 解を求めると,
の二次方程式として, 解を求めると, ![]()
これを変形すると![]() なので,
なので, 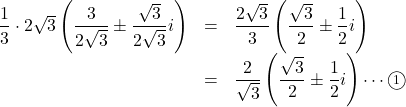
よって, ![]() ,
, ![]() となる
となる![]() は
は![]() なので,
なので, ![]() は
は![]() (答)
(答)
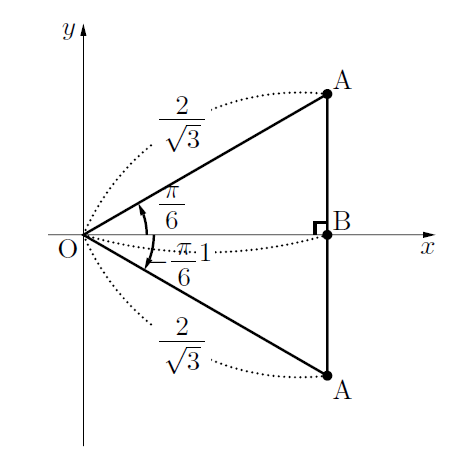
(2) (1)より![]()
と変形できるので, OAはOBを![]() 倍に拡大し,
倍に拡大し, ![]() または,
または, ![]() 回転させたものである。このとき, △OABは
回転させたものである。このとき, △OABは![]() の直角三角形になる。(下図参照)
の直角三角形になる。(下図参照)
よって, ![]() ,
, ![]()
となる。
 数樂管理人のブログ
数樂管理人のブログ