こんにちは。今回は複素数の問題で![]() の
の![]() 乗根の求め方について書いておきます。例題を解きながら見ていきましょう。
乗根の求め方について書いておきます。例題を解きながら見ていきましょう。
【例】1の6乗根を求めよ。
【解法】求める複素数を![]() とおく。ただし,
とおく。ただし, ![]() 。
。
このとき, ![]() を6乗すると,
を6乗すると, ![]()
ここで, 1を極形式で表すと,![]()
![]() なので,
なので, ![]()
これより, ![]()
![]() (
(![]() は整数)
は整数)![]() より,
より, ![]()
![]() より,
より, ![]() なので,
なので, ![]() 。これを満たす
。これを満たす![]() の値は,
の値は, ![]()
このとき![]() は,
は, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() となるので,
となるので, ![]()
したがって求める複素数は, 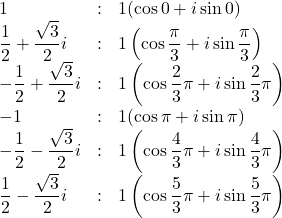
(答) ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
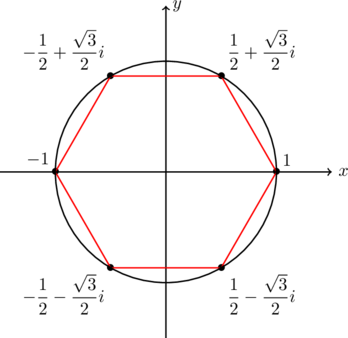
複素数平面上で解の配置を見ると正六角形になっています。
n乗根の求め方
![]()
![]() ただし,
ただし, ![]() とおく。
とおく。![]()
![]() を
を![]() を用いて極形式で表す。
を用いて極形式で表す。![]()
![]() の
の![]() を極形式で表す。
を極形式で表す。![]()
![]() として, (極形式)=(極形式)とする。
として, (極形式)=(極形式)とする。![]()
![]() で絶対値と偏角を比べ求める。偏角は
で絶対値と偏角を比べ求める。偏角は![]() の整数倍を加えるのを忘れずに。
の整数倍を加えるのを忘れずに。![]()
![]() で求めた絶対値と偏角を用いて
で求めた絶対値と偏角を用いて![]() を求める。
を求める。
n乗根の解の配置
![]() 乗根の解の配置は複素数平面上で正
乗根の解の配置は複素数平面上で正![]() 角形をつくる。
角形をつくる。
最後に例題をもう一題やって終わりにしましょう。
【例】![]() を満たす複素数
を満たす複素数![]() を求めよ。
を求めよ。
【解法】
上の流れに沿ってみましょう。![]() とおく。ただし,
とおく。ただし, ![]()
![]()
![]()
![]()
![]() より,
より, ![]()
![]()
![]() なので,
なので, ![]() より,
より, ![]() 。
。
これを満たす![]() は
は![]()
このとき, ![]() を求めると,
を求めると, ![]()
よって求める複素数![]() は,
は, ![]()
![]()
![]()
以上より
(答) ![]()
複素数平面上で解の配置を見ると正三角形になっています。

 数樂管理人のブログ
数樂管理人のブログ 

