こんにちは。今回は空間における4点の座標がわかる場合の四面体の体積を求めてみたいと思います。例題を解きながら見ていきます。
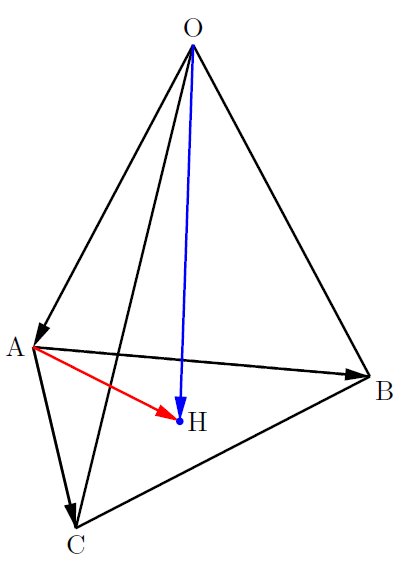
【例】原点と3点A(1, 0, 0), B(1, 2, 3), C(0, 1, 2)を頂点とする四面体OABCの体積を求めよ。
【解法】原点から△ABCに下ろした垂線を![]() とします。また,
とします。また, ![]() である。
である。
このとき, ![]() を実数とすると,
を実数とすると, 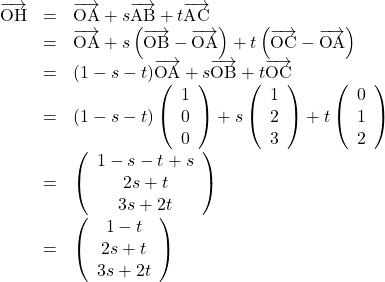
ここで, ![]() で,
で, ![]() ,
, ![]() であるから,
であるから, 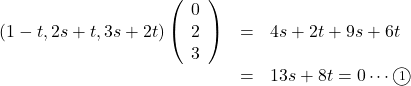
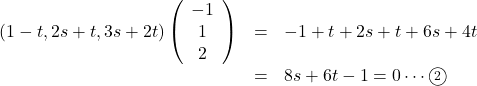
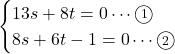
これを解いて, ![]()
よって, ![]() は,
は, 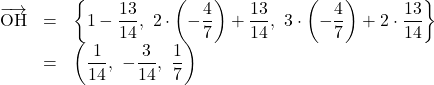
となるので, ![]() の大きさは,
の大きさは, 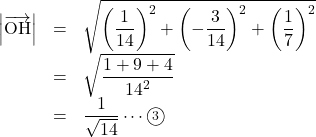
となる。
△ABCの面積は, ![]() なので,
なので, ![]()
![]()
![]() と
と![]() の内積は,
の内積は, 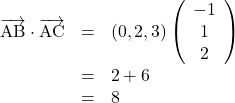
したがって, 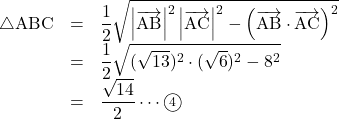
![]() より, 求める体積は
より, 求める体積は![]() (答)
(答)
四面体の体積の攻略を以下にまとめました。結構ベクトルと四面体の体積ではこの手法は有効だと思うので, 身に付けておいてくださいね。
四面体の体積の攻略(ベクトル)
![]()
![]() (高さ)を
(高さ)を![]() とおく。
とおく。![]()
![]() ,
, ![]() から内積0を使って
から内積0を使って![]() の連立方程式をつくり, 解く。
の連立方程式をつくり, 解く。![]()
![]() から
から![]() を求め,
を求め, ![]() を求める。
を求める。![]()
![]() ,
, ![]() などを用いて,
などを用いて, ![]() の面積を求める。
の面積を求める。![]()
![]() を用いて四面体の体積を求める。
を用いて四面体の体積を求める。
※![]() の式は
の式は![]() から導ける。
から導ける。
 数樂管理人のブログ
数樂管理人のブログ