こんにちは。相城です。この記事は書こうか, 書くまいか迷ったのですが, 皆さんの意見も聞きたくて書くことにしました。基礎学でのあるあると言えばそれまでなんですが。もう採点も終わって採点がひっくり返るということはないでしょうけど, もし以下のように考える生徒がいたとしたらむごい問題だと思ったので, 書いておきます。私が問題視しているのは次の問題です。
どちらの再生時間?
たかしさんは, タブレット型PC端末を使って, 理科と数学に関する動画を1本ずつ再生した。理科と数学の動画の再生時間の合計は5分45秒だが, 理科の動画を0.75倍速で再生し, 数学の動画を1.5倍速で再生したところ, 動画の再生時間の合計が5分30秒になった。次の(1)~(3)に答えなさい。
※6分の動画を2倍速で再生すると, 再生時間は3分になる。
(1) 4分10秒の動画を0.5倍速で再生すると, 再生時間は何分何秒になるか求めなさい。
(2) 理科の動画の再生時間を![]() 分, 数学の動画の再生時間を
分, 数学の動画の再生時間を![]() 分として, 連立方程式をつくりなさい。
分として, 連立方程式をつくりなさい。
(3) (2)の連立方程式を解き, 理科と数学の動画の再生時間はそれぞれ何分何秒になるか求めなさい。
【令和3年第一回徳島県基礎学力テスト】
はじめ大人の先入観でハイハイ0.75![]() で割って, 1.5
で割って, 1.5![]() で割って式つくればいいんでしょってな感じで, 正答を得たのですが, 本日再考してみると, いや待てよ, 再生時間って0.75倍速や1.5倍速の再生時間と考えてもいいよね?だって問題文には再生時間をとしか書いていないので, その再生時間が通常の再生時間なのか, 倍速の再生時間なのか一意に決まらないことないですか?(1)の問いにも0.5倍速にすると, 再生時間は
で割って式つくればいいんでしょってな感じで, 正答を得たのですが, 本日再考してみると, いや待てよ, 再生時間って0.75倍速や1.5倍速の再生時間と考えてもいいよね?だって問題文には再生時間をとしか書いていないので, その再生時間が通常の再生時間なのか, 倍速の再生時間なのか一意に決まらないことないですか?(1)の問いにも0.5倍速にすると, 再生時間は![]() としか書いてないですから。ですから生徒によっては, 理科と数学の倍速の再生時間を
としか書いてないですから。ですから生徒によっては, 理科と数学の倍速の再生時間を![]() ,
, ![]() として次のように式をつくったかもしれません。
として次のように式をつくったかもしれません。
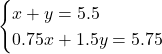
これを解いて![]()
よって再生時間は理科3分20秒, 数学2分10秒としても差し支えない気がするのですが![]()
一意性を持たせるなら, 理科の通常の再生時間を![]() 分など再生時間に関する補足がいると思うのですが。
分など再生時間に関する補足がいると思うのですが。
これは個人的な感想ですので, 間違いがあれば仰ってください。訂正もしくは削除します。
 数樂管理人のブログ
数樂管理人のブログ 


6分を2倍速にすると3分になるということは、2倍になると時間が半分、0.5倍になると時間が2倍になると捉えることができると思います。
もとの再生時間をそれぞれx,yとした時、私の考えとしては、0.75倍で再生するとかかる時間が4/3倍となるので、4/3x、1.5倍再生するとかかる時間は2/3倍となるので2/3yとし、4/3x+2/3y=22/4を一つ目の式、x+y=23/4を2つ目の式として計算してみました。
これを解いた結果、理科(x)が2分30秒、数学(y)が3分15秒となりました。
実際の解答は分かりませんが、何が正解なのでしょうか。少し疑問は残りますね。。。
通りすがりの大学生さん。コメントありがとうございます。
さて、貴君の解答が正当になっているのですが、解釈として私の解答もアリかな?と思うので、記事を書きました。
私の解釈も許されるのであれば、生徒の進路にかかわるテストなので、慎重に作問していただきたいと願います。