こんにちは。今回は3項間漸化式をやってみましょう。
3項間漸化式の問題
【問題】次の条件によって定められる数列![]() の一般項を求めよ。
の一般項を求めよ。
(1) ![]()
(2) ![]()
(3) ![]()
【解答】
(1) 特性方程式![]() を解くと
を解くと![]() ,
, ![]()
これを参考に漸化式を変形する。(※特性方程式のことは答案には書かない)
漸化式 ![]() を変形すると,
を変形すると, ![]() となる。
となる。
数列![]() は, 初項
は, 初項![]() , 公比
, 公比![]() の等比数列であるから,
の等比数列であるから, ![]()
したがって, ![]() のとき,
のとき, 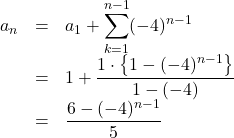
これは![]() のときも成り立つ。
のときも成り立つ。
よって, ![]() (答)
(答)
(2) 特性方程式![]() を解くと
を解くと![]() ,
, ![]()
これを参考に漸化式を変形する。(※特性方程式のことは答案には書かない)
漸化式![]() を変形すると,
を変形すると, ![]()
または, ![]()
となる。![]() のとき,
のとき,
数列![]() は初項
は初項![]() , 公比3の等比数列なので,
, 公比3の等比数列なので, ![]()
![]() のとき,
のとき,
数列![]() は初項
は初項![]() , 公比2の等比数列なので,
, 公比2の等比数列なので, ![]()
![]() より,
より, ![]() (答)
(答)
(3) 特性方程式 ![]() を解くと
を解くと![]() ,
, ![]()
これを参考に漸化式を変形する。(※特性方程式のことは答案には書かない)
漸化式![]() を変形すると,
を変形すると, ![]() となる。
となる。
数列![]() は, 初項
は, 初項![]() , 公比4の等比数列であるから,
, 公比4の等比数列であるから, ![]()
![]() の両辺を
の両辺を![]() で割ると,
で割ると, ![]()
これより, ![]()
したがって, 数列![]() は, 初項
は, 初項![]() , 公差
, 公差![]() の等差数列である。
の等差数列である。
よって, 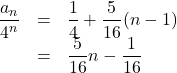
ゆえに, 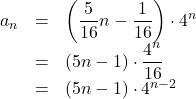
![]() (答)
(答)
 数樂管理人のブログ
数樂管理人のブログ 


