こんにちは。今回は数列や積分などで頻出の分子が1の部分分数の求め方について書いておきます。分母が2次式で, 因数分解できるものに限って書いておきます。
よく出題されるのが分子が1の問題です。
【例】![]() を部分分数分解しなさい。
を部分分数分解しなさい。
【解答】![]()
実は分子が1で分母の![]() の係数がそろっているときは, 次のような公式があります。
の係数がそろっているときは, 次のような公式があります。![]()
特に![]() のときは頻出で,
のときは頻出で,
![]()
となります。
【公式の導出】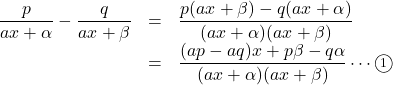
![]() で
で![]() の係数が0になるためには,
の係数が0になるためには, ![]() であればよい。このとき,
であればよい。このとき, ![]() は次のように書ける。
は次のように書ける。![]()
![]() の分子を1にするためには,
の分子を1にするためには, ![]() をかけてやればよい。
をかけてやればよい。
したがって, それをかけることによって,
![]()
を得る。
【例】 ![]() を部分分数分解しなさい。
を部分分数分解しなさい。
【解答】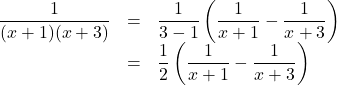
分子が1になるものはよく出題されるので押さえておきたいテクニックですね。
分母が2式からできて, 分子が1の場合,
公式![]()
特に![]() のときは,
のときは,![]()
を使うとうまく分解できる。
分母が3つの数の積で表された分数を部分分数分解する問題も頻出系としてあります。次の例を見ておきましょう。
【例】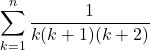 を求めよ。
を求めよ。
【解法】数列の場合, 分母を1つ1つの式で分解するのではなく, 式を連続する2数(k(k+1)), 連続する2数((k+1)(k+2))に分けて部分分数分解します。
すると, ![]()
と分解でき, 分数計算が以下のように楽になります。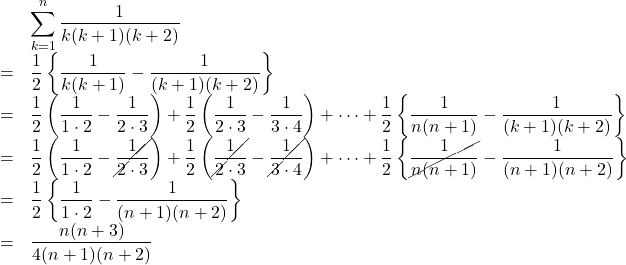
となります。
数列の場合, 分母が3つの式からなる場合は, 3式の大小関係から, 分母を小中の2式, 中大の2式で部分分数分解する。その結果, 分子が定数になれば, 定数の逆数をかけるように調整するとうまくいく。
数IIIの積分などでは, 分母を3つに分けた方が楽な場合がある。
【公式】![]()
![]()
【例】上の公式ができることを示せ。![]() と表せるとすると,
と表せるとすると, 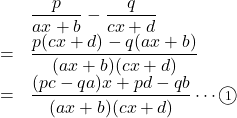
![]() の分子を1にするためには, 分子の
の分子を1にするためには, 分子の![]() の係数が0でなくてはならない。このとき,
の係数が0でなくてはならない。このとき, ![]() とすることで,
とすることで, ![]() の係数は0にできる。
の係数は0にできる。
このとき, ![]() は次のように書ける。
は次のように書ける。![]()
したがって, 分子を1にするためには, この式に![]() をかけるとよい。
をかけるとよい。
以上のことから,
![]()
を得る。
【例】![]() を部分分数分解せよ。
を部分分数分解せよ。
【解法】![]() とすると, 公式より
とすると, 公式より![]()
となるので, ![]()
となる。
はじめに示した公式などはこの公式からすべて導くことができることは明らかである。
一般的な部分分数分解はこちらの記事をご覧ください。
 高校数学:部分分数分解の分け方のパターン
高校数学:部分分数分解の分け方のパターン 数樂管理人のブログ
数樂管理人のブログ 

