今回は球をある平面で切ったときにできる円の方程式を求めていきましょう。例題を解きながらいきましょう。
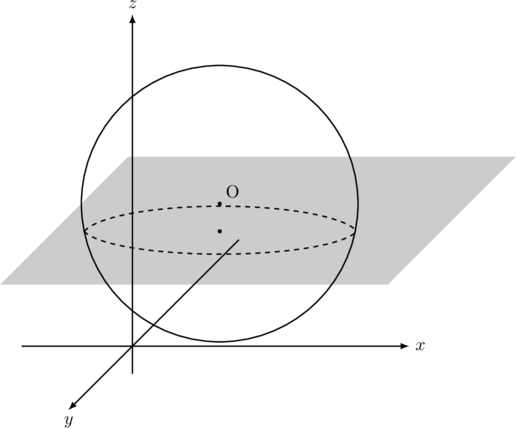
【例題】球面O ![]() と平面
と平面![]() が交わってできる部分は円になります。その円の方程式を求めよ。
が交わってできる部分は円になります。その円の方程式を求めよ。
【解法】交わる部分は, ![]() を満たすのだから, 球面の方程式に
を満たすのだから, 球面の方程式に![]() を代入する。
を代入する。
![]()
![]()
![]()
よって, 中心![]() , 半径
, 半径![]() の円
の円
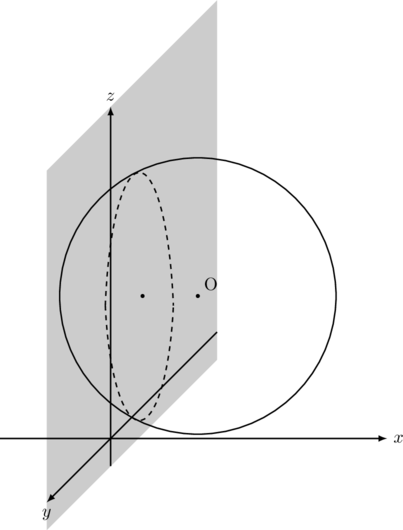
【例題】 球面O ![]() と
と![]() 平面が交わってできる部分は円になります。その円の方程式を求めよ。
平面が交わってできる部分は円になります。その円の方程式を求めよ。
【解法】交わる部分は, ![]() を満たすのだから, 球面の方程式に
を満たすのだから, 球面の方程式に![]() を代入する。
を代入する。
![]()
![]()
![]()
よって, 中心![]() , 半径
, 半径![]() の円
の円
解法のコツ
平面の条件である値を球面の方程式に代入して, 円の方程式を求める。
 数樂管理人のブログ
数樂管理人のブログ 

