TikZ：高校数学：二次関数と二次方程式の解②

こんにちは。今回は2次関数と2次方程式の解ということで, 2次方程式の解の範囲をグラフ的に捉えて解決していきましょう。最後に数IIでの解法も載せておきます。

例題

【例題】2次方程式 $2x^2-4mx+m+3=0$ が, 次のような解をもつとき, 定数 $m$ の範囲を求めよ。
(ア)　異なる2つの解がともに1より大きいとき
(イ)　異なる2つの解がともに1より小さいとき
(ウ)　1つの解が1より大きく, 他の解が1より小さいとき

(ア)の解法

$f(x)=2x^2-4mx+m+3$ とおく。 $x$ の関数 $f(x)$ のグラフと $x$ 軸との交点が2次方程式の解になることを利用して解いていく。このとき, 関数 $f(x)$ のイメージとしては以下のようになればよい。

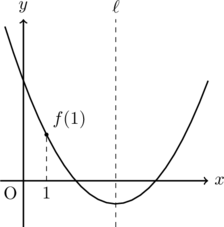
解決方法は次の3つを調べること。
それは, 判別式, 軸, $f(1)$ の値。この場合この3つに与えられる条件はグラフから以下のようである。
判別式 $(D)>0$ (異なる2つの実数解を持つ条件)
軸 $(\ell)>1$ (軸が $x=1$ より右側にあること)
$f(1)>0$ ( $D>0$ かつ軸が $x=1$ より右側にあれば, この条件を加えることで解が2つとも $x=1$ より右側にあることになる。)
この3つを同時に満たすことで, $f(x)$ は $x$ 軸の1より大きいところで, 異なる2点で交わることになります。つまり, 題の二次方程式の異なる2つの解は1より大きいことになります。
まず, 判別式 $D/4=(2m)^2-2(m+3)=4m^2-2m-6>0$ より, 2で割って因数分解すると,
$(m+1)(2m-3)>0$
$m<-1, m>\dfrac32\cdots\maru1$
次に軸に関して,
$f(x)$ を平方完成すると, $f(x)=2(x-m)^2-2m^2+m+3$ となるので,
軸の式は $x=m$ 。
これが1より大きいことが条件なので, $m>1\cdots\maru2$
最後に, $f(1)>0$ より, $f(1)=-3m+5$ であるから,
$-3m+5>0$ , $m<\dfrac53\cdots\maru3$
$\maru1, \maru2, \maru3$ の共通範囲を求めると,
$\dfrac32<m<\dfrac53\cdots$ (答)

(イ)の解法

(イ)の解法
(ア)の解法同様, グラフを描いてイメージをつかむ。
このとき, 関数 $f(x)$ のイメージとしては以下のようになればよい。

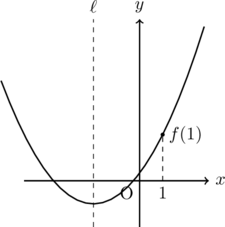
解決方法は次の3つを調べること。
それは, 判別式, 軸, $f(1)$ の値。この場合この3つに与えられる条件はグラフから以下のようである。
判別式 $(D)>0$ (異なる2つの実数解を持つ条件)
軸 $(\ell)<1$ (軸が $x=1$ より左側にあること)
$f(1)>0$ ( $D>0$ かつ軸が $x=1$ より左側にあれば, この条件を加えることで解が2つとも $x=1$ より左側にあることになる。)
この3つを同時に満たすことで, $f(x)$ は $x$ 軸の1より小さいところで, 異なる2点で交わることになります。つまり, 題の二次方程式の異なる2つの解は1より小さいことになります。
まず, 判別式 $D/4=(2m)^2-2(m+3)=4m^2-2m-6>0$ より, 2で割って因数分解すると,
$(m+1)(2m-3)>0$
$m<-1, m>\dfrac32\cdots\maru1$
次に軸に関して,
$f(x)$ を平方完成すると, $f(x)=2(x-m)^2-2m^2+m+3$ となるので,
軸の式は $x=m$ 。
これが1より小さいことが条件なので, $m<1\cdots\maru2$
最後に, $f(1)>0$ より, $f(1)=-3m+5$ であるから,
$-3m+5>0$ , $m<\dfrac53\cdots\maru3$
$\maru1, \maru2, \maru3$ の共通範囲を求めると,
$m<-1\cdots$ (答)

(ウ)の解法

(ウ)の解法
これまでと同様にグラフを描いてイメージをつかむ。

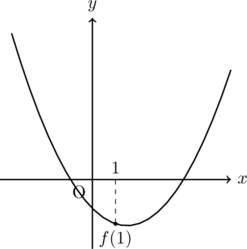
上の図からわかるように, 1つの解は1より大きく, 他の解は1より小さい場合では, $f(1)$ の値が負であれば, 題を満たすことになる。したがって, $f(1)<0$ が条件になる。
$f(1)=-3m+5$ であるから, $-3m+5<0$ , $m>\dfrac53$ となるので, 求める範囲は,
$m>\dfrac53\cdots$ (答)

思考のロジックはこれと同じ

考え方は2次関数と2次方程式①と同じで, この①では0より大きい異なる2解だったのが今回は1より大きい異なる2解に変わっただけである。0より小さい異なる2解も同じこと。正と負の解については, 0より大きい解と0より小さい解と言い換えれば, 今回のものは1より大きい解と１より小さい解となっただけである。