こんにちは。頻出系の式変形を書いておきます。知らないとこんな式変形思いつかないかもという内容です。先ず例題を示します。そして, 最後に類題をやってみましょう。
【例題】複素数![]() が
が![]() のとき,
のとき,
(1) ![]() の値を求めよ。
の値を求めよ。
(2) ![]() の値を求めよ。
の値を求めよ。
【解法】
(1) ![]() の両辺を5乗する。5乗する理由は偏角を
の両辺を5乗する。5乗する理由は偏角を![]() にするためである。
にするためである。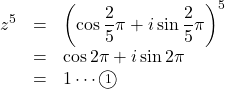
![]() から,
から, ![]() となり,
となり, ![]() として, 左辺を因数分解すると,
として, 左辺を因数分解すると, ![]()
となる。このとき, ![]() なので,
なので, ![]() である。
である。
よって, ![]()
したがって, 求める値は0である。
(2) ![]() に指数法則を用いると,
に指数法則を用いると, ![]()
したがって, 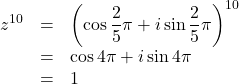
よって, 求める値は1である。
知っておきたいテクニック
![]() 両辺を何乗かして
両辺を何乗かして![]() をつくる。
をつくる。![]() 因数分解のテクニック
因数分解のテクニック![]() の因数分解(ちゃんと因数分解すると
の因数分解(ちゃんと因数分解すると![]() の値によっては以下のようにならないこともあります。)
の値によっては以下のようにならないこともあります。)![]()
例 ![]()
例外 ![]()
ただし, これも, ![]() と変形はできます。
と変形はできます。
【類題】複素数![]() が
が![]() のとき, 次の値を求めよ。
のとき, 次の値を求めよ。
(1) ![]()
(2) ![]()
【略解】
(1) ![]() の両辺を26乗すると,
の両辺を26乗すると, ![]()
![]()
![]()
![]() より,
より, ![]()
つまり, ![]()
よって求める値は![]()
(2) ![]()
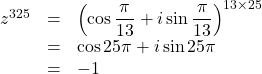
よって求める値は![]()
 数樂管理人のブログ
数樂管理人のブログ 

