こんにちは。今回は無理関数の積分について書いておきます。以下, ![]() は積分定数とします。
は積分定数とします。
![]() や
や![]() の積分では,
の積分では, ![]() とおくとうまくいくことが多い。
とおくとうまくいくことが多い。
【例1】![]() の不定積分を求めよ。
の不定積分を求めよ。![]() とおくと,
とおくと, ![]() より,
より, ![]()
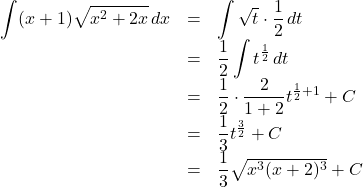
【例2】![]() の不定積分を求めよ。
の不定積分を求めよ。![]() とおくと,
とおくと, ![]() より,
より, ![]()
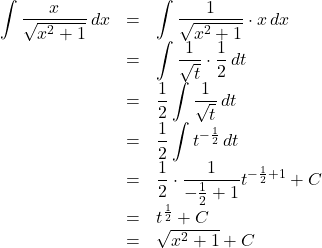
上記のような関係がない場合, つまり, ![]() や
や![]() の積分では,
の積分では, ![]() とおくとうまくいくことが多い。
とおくとうまくいくことが多い。
【例】![]() の不定積分を求めよ。
の不定積分を求めよ。![]() とおいて, 両辺2乗すると,
とおいて, 両辺2乗すると, ![]() なので,
なので, ![]() , また,
, また, ![]() なので,
なので, 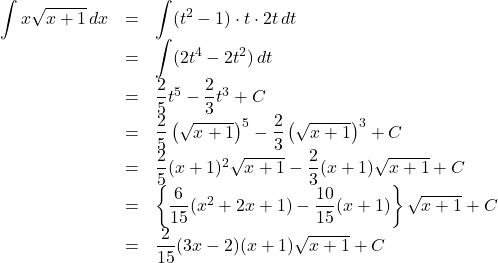
分母が![]() の場合, 有理化を行って処理していくことが多い。
の場合, 有理化を行って処理していくことが多い。
【例】![]() の不定積分を求めよ。
の不定積分を求めよ。
積分される関数の分母を有理化すると, 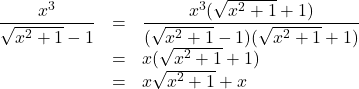
となるので, 与式は![]()
となる。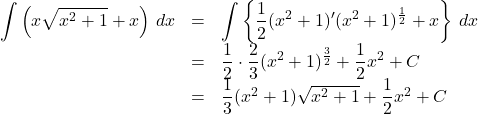
これでもうまくいかない場合は, 次の部分分数分解という手段が考えられる。
【例】不定積分![]() を次のようにして求めよ。
を次のようにして求めよ。
(1) ![]() となる, 定数
となる, 定数![]() を求めよ。
を求めよ。
(2) (1)を利用し, 問題の不定積分を求めよ。
【解法例】
(1)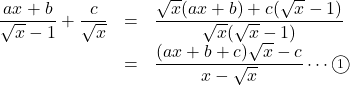
![]() と与式の
と与式の![]() が恒等的な関係なので,
が恒等的な関係なので,![]() ,
, ![]()
よって, ![]() ,
, ![]() ,
, ![]()
(2) (1)より, ![]()
となり, 右辺の左の項を有理化すると, ![]()
よって求める不定積分は, 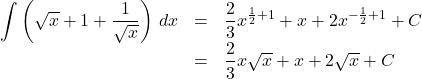
 数樂管理人のブログ
数樂管理人のブログ 


数Ⅲ積分 無理数の積分2番目の解答は
途中ではないかと思います。
私はこの授業が大好きです。
こんにちは。
お世話になります。
恥ずかしながらどの番号のことかわかりません。
詳しく教えていただけないでしょうか。
よろしくお願いします。
根号の中と外の式でf'(x),f(x)の関係がない場合で解答が5分の2と3分の2で終わっていますが分母を15に揃えるのが良いのか?私は先生の解答の方が理解しやすいです。今後も勉強させて頂きます。良きアドバイス宜しくお願い致します。
こんにちは。
ご指摘ありがとうございます。
修正しましたのでご確認よろしくお願いします。
今後とも何かございましたらアドバイスください。
よろしくお願いします。