こんにちは。今回は三角関数の積分について書いておきます。以下, ![]() は積分定数とします。
は積分定数とします。
基本的な考え方は次のような感じです。![]() は
は![]() とおけば,
とおけば, ![]() となるので,
となるので, ![]() と書き換えできる。
と書き換えできる。
したがって, ![]() ,
, ![]() なので,
なので, ![]() で
で![]() とおくと,
とおくと, ![]() なので,
なので,
(与式)![]() となる。
となる。
同様に, ![]() で
で![]() とおくと,
とおくと, ![]() なので,
なので,
(与式)![]() となる。
となる。
![]() ,
, ![]() ,
, ![]() は,
は,![]() や 2倍角の公式を用いて,
や 2倍角の公式を用いて, ![]() ,
, ![]() を用いた式に書き換えて積分するのが定石です。
を用いた式に書き換えて積分するのが定石です。![]()
![]() から,
から, ![]()
![]()
![]() から,
から, ![]()
![]()
![]() から,
から, ![]()
などを用いる。
【例】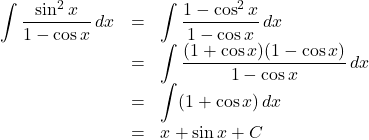
![]() や
や![]() の奇数乗の積分では次のように処理するとうまくいくことがある。
の奇数乗の積分では次のように処理するとうまくいくことがある。![]()
![]() として,
として, ![]() で置換する。
で置換する。![]()
![]() として,
として, ![]() で置換する。
で置換する。
【例】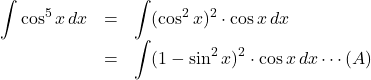
ここで, ![]() とおくと,
とおくと, ![]() なので,
なので,
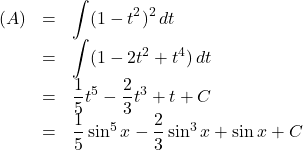
三角関数の積の積分は積和の公式で和の式に直して積分する。
積和の公式![]()
![]()
![]()
![]()
![]()
![]()
【例】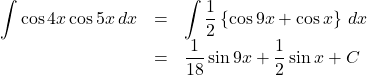
積和の公式については以下の記事をご覧ください。
 高校数学:積和の公式とその導出
高校数学:積和の公式とその導出 数樂管理人のブログ
数樂管理人のブログ 
