こんにちは。今回は合成関数の微分について書いておきます。
合成関数は![]() と表される関数ですが, ここではわかりやすく,
と表される関数ですが, ここではわかりやすく, ![]() とします。このとき, 合成関数
とします。このとき, 合成関数![]() は
は![]() となり,
となり, ![]() は
は![]() の関数で,
の関数で, ![]() は
は![]() の関数です。この場合,
の関数です。この場合, ![]() は次のように変形して求められます。
は次のように変形して求められます。![]()
![]() の
の![]() を
を![]() ,
, ![]() を
を![]() で置き換えると,
で置き換えると, ![]()
となります。
これは, 関数![]() をそのまま微分して, その後, 関数
をそのまま微分して, その後, 関数![]() の中身を微分してかけることを意味しています。
の中身を微分してかけることを意味しています。
特に, ![]()
が成り立つ。
実際に例題をやってみましょう。
【例】関数![]() を微分せよ。
を微分せよ。
【解答】上の説明で![]() にあたるのが,
にあたるのが, ![]() なので,
なので, ![]() として,
として, ![]() で微分すると,
で微分すると, ![]()
となって, 次に![]() を
を![]() で微分して,
で微分して, ![]()
となるので, 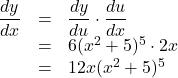
となります。
次に上の![]() を使った解答例を示します。
を使った解答例を示します。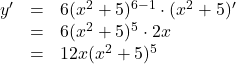
となります。
【例】関数![]() を微分せよ。
を微分せよ。
【解答】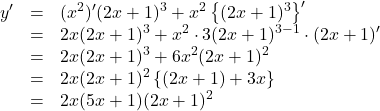
![]() は
は![]() として微分を行うとよい。
として微分を行うとよい。
また, ![]() は
は![]() として微分を行うとよい。
として微分を行うとよい。
この2つの微分においての考え方は前述した上の![]() の方法で行うものとします。
の方法で行うものとします。
例題をやってみましょう。
【例】関数![]() を微分せよ。
を微分せよ。
【解答】![]() なので,
なので, ![Rendered by QuickLaTeX.com \begin{array}{lll}y'&=&\dfrac{5}{3}\cdot x\right^{\frac53-1}\cdot(x)'\\&=&\dfrac{5}{3}\cdot x\right^{\frac23}\cdot1\\&=&\dfrac{5}{3}\sqrt[3]{x^2}\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-c47995e30c8dadc1203af11759a22056_l3.png)
【例】関数![]() を微分せよ。
を微分せよ。
【解答】![]() なので,
なので, ![Rendered by QuickLaTeX.com \begin{array}{lll}y'&=&-\dfrac13(3x-1)^{-\frac13-1}\cdot(3x-1)'\\&=&-\dfrac13(3x-1)^{-\frac43}\cdot3\\&=&-\dfrac{1}{(3x-1)\sqrt[3]{3x-1}}\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-bcef617c0e53ae6317066fbff8f28ac1_l3.png)
【例】関数![]() を微分せよ。
を微分せよ。
【解答】![]() なので,
なので, 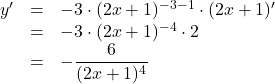
 数樂管理人のブログ
数樂管理人のブログ 

