こんにちは。今回は微分しても変わらない![]() について書いておきます。
について書いておきます。
![]() の定義は,
の定義は, ![]()
である。
詳しくはこちらの記事を参照ください。
さて, ![]() の両辺の自然対数をとると,
の両辺の自然対数をとると, 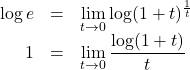
よって, ![]()
![]() の式で,
の式で, ![]() とおくとき,
とおくとき, ![]() なら,
なら, ![]() であり,
であり, ![]() であるから,
であるから, ![]() 式の左辺は次のように書ける。
式の左辺は次のように書ける。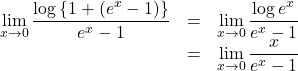
よって, ![]()
ここで, 左辺の分母分子を入れ換えても値は変わらないので, ![]()
となる。
ここで, 関数![]() を導関数の定義にしたがって微分すると,
を導関数の定義にしたがって微分すると, 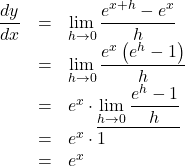
このように, ![]() は微分しても
は微分しても![]() となるわけである。
となるわけである。
※下線部は![]() から
から![]() となる。
となる。
こんにちは。今回は微分しても変わらない![]() について書いておきます。
について書いておきます。
![]() の定義は,
の定義は, ![]()
である。
詳しくはこちらの記事を参照ください。
さて, ![]() の両辺の自然対数をとると,
の両辺の自然対数をとると, 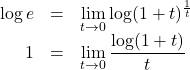
よって, ![]()
![]() の式で,
の式で, ![]() とおくとき,
とおくとき, ![]() なら,
なら, ![]() であり,
であり, ![]() であるから,
であるから, ![]() 式の左辺は次のように書ける。
式の左辺は次のように書ける。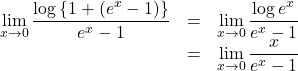
よって, ![]()
ここで, 左辺の分母分子を入れ換えても値は変わらないので, ![]()
となる。
ここで, 関数![]() を導関数の定義にしたがって微分すると,
を導関数の定義にしたがって微分すると, 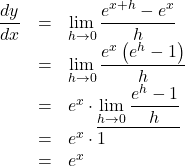
このように, ![]() は微分しても
は微分しても![]() となるわけである。
となるわけである。
※下線部は![]() から
から![]() となる。
となる。