こんにちは。今回は円や楕円といった関数![]() の微分法について書いておきます。
の微分法について書いておきます。
![]() で表される関数を
で表される関数を![]() について微分すると,
について微分すると, ![]() となり,
となり, ![]() なので,
なので, ![]() (複合同順)
(複合同順)
となる。
次の式から![]() を求めよ。ただし,
を求めよ。ただし, ![]() を用いてもよい。
を用いてもよい。
![]()
【解答】![]()
![]() (答)
(答)
![]()
【解答】![]()
![]()
![]() (答)
(答)
![]()
【解答】![]()
![]()
![]() (答)
(答)
![]() で表される関数を
で表される関数を![]() について微分すると,
について微分すると, ![]() となり,
となり, 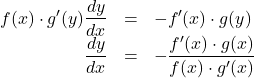
よって, ![]()
次の式から![]() を求めよ。ただし,
を求めよ。ただし, ![]() を用いてもよい。
を用いてもよい。
![]()
【解答】![]()
![]()
![]() (答)
(答)
![]()
【解答】![]()
![]()
![]() (答)
(答)
![]()
【解答】![]()
![]() として,
として, ![]() (答)
(答)
こんにちは。今回は円や楕円といった関数![]() の微分法について書いておきます。
の微分法について書いておきます。
![]() で表される関数を
で表される関数を![]() について微分すると,
について微分すると, ![]() となり,
となり, ![]() なので,
なので, ![]() (複合同順)
(複合同順)
となる。
次の式から![]() を求めよ。ただし,
を求めよ。ただし, ![]() を用いてもよい。
を用いてもよい。
![]()
【解答】![]()
![]() (答)
(答)
![]()
【解答】![]()
![]()
![]() (答)
(答)
![]()
【解答】![]()
![]()
![]() (答)
(答)
![]() で表される関数を
で表される関数を![]() について微分すると,
について微分すると, ![]() となり,
となり, 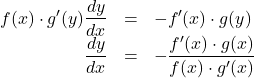
よって, ![]()
次の式から![]() を求めよ。ただし,
を求めよ。ただし, ![]() を用いてもよい。
を用いてもよい。
![]()
【解答】![]()
![]()
![]() (答)
(答)
![]()
【解答】![]()
![]()
![]() (答)
(答)
![]()
【解答】![]()
![]() として,
として, ![]() (答)
(答)