こんにちは。今回は, グラフ問題の解法のテクニックをご紹介します。
まずこの問題が解けるか考えてみましょう。
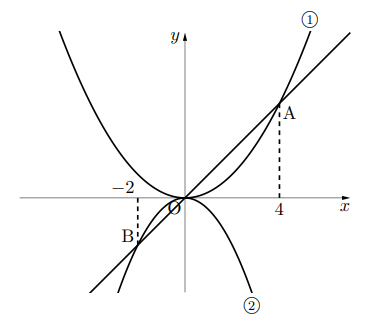
右の図のように, 関数![]() ,
, ![]() が原点を通る直線と2点A, Bで, それぞれ交わっている。
が原点を通る直線と2点A, Bで, それぞれ交わっている。
A, Bの![]() 座標が, それぞれ
座標が, それぞれ![]() ,
, ![]() であるとき, 次の問いに答えなさい。
であるとき, 次の問いに答えなさい。
(1) ![]() の値を求めなさい。
の値を求めなさい。
放物線の式を求めたければ, 放物線![]() 上の点の座標が1つ(原点は除く)分かればよい。この場合は, Aの座標が分かればよさそうなことに着眼する。
上の点の座標が1つ(原点は除く)分かればよい。この場合は, Aの座標が分かればよさそうなことに着眼する。
関数の問題は, 僕自身が思っている, 分かっているものをどう使っていくかがポイントであるということ。
どうしても分ってないものを使う場合は文字で置く。これを基本スタイルとして, 問題に反映させていく。
まず, ここで分かっているものは![]() と点A, Bの
と点A, Bの![]() 座標の4,
座標の4, ![]() である。
である。
Bが![]() 上にあるので,
上にあるので, ![]() を
を![]() に代入して, B
に代入して, B![]() を得る。このBの座標は今分かったので, それを使って原点を通る直線の式(比例の式)を
を得る。このBの座標は今分かったので, それを使って原点を通る直線の式(比例の式)を![]() として求める。B
として求める。B![]() を
を![]() に代入して,
に代入して, ![]() を得る。これによって, 原点を通る直線の式は
を得る。これによって, 原点を通る直線の式は![]() と分かった。これも今分かったので使う。Aはこの
と分かった。これも今分かったので使う。Aはこの![]() 上の点でもあるから,
上の点でもあるから, ![]() を
を![]() に代入すると, A
に代入すると, A![]() を得る。これで
を得る。これで![]() 上の点Aの座標がA
上の点Aの座標がA![]() と分かったので, これを
と分かったので, これを![]() に代入して
に代入して![]() (答)を得る。
(答)を得る。
このように, 1つ分かったら次, 次が分かったらその次という具合にドミノ式に分かってくる。基本パターンはこんな感じですので, 解き方のご参考にしてください。
攻略法
分かってるものを使ってドミノ式で片づける。
 数樂管理人のブログ
数樂管理人のブログ