こんにちは。高2の数列, 高3の積分などで活躍すると思われる部分分数分解。その分け方のパターンを見ていこうと思います。出てくる形は大体これというものを書いておきます。以下, 2パターンを紹介しておきます。
部分分数分解の方法として, 例えば, ![]() を部分分数に分ける場合,
を部分分数に分ける場合, ![]()
とおいて, 右辺を通分し, 分子の係数比較を行うことで, 連立方程式ができ, それを解くことで, 定数![]() の値が求まり, 部分分数分解を実現できる仕組みになります。この他に, 分母をはらって恒等的な関係を用いる数値代入法で, 定数
の値が求まり, 部分分数分解を実現できる仕組みになります。この他に, 分母をはらって恒等的な関係を用いる数値代入法で, 定数![]() の値が求まります。考え方自体は恒等式の攻め方と同じです。
の値が求まります。考え方自体は恒等式の攻め方と同じです。
【例】部分分数に分解すると, ![]() となる。定数
となる。定数![]() の値を求めよ。
の値を求めよ。
【解法1】係数比較
右辺を通分すると, ![]()
これが左辺と等しいので, ![]() ,
, ![]() となり, これを解くと,
となり, これを解くと, ![]()
※通分でなくとも, 両辺に![]() をかけて行ってもよい。
をかけて行ってもよい。
【解法2】数値代入法
与式の両辺に![]() をかけて,
をかけて, ![]()
![]() とすると,
とすると, ![]()
![]() とすると,
とすると, ![]()
これを解くと, ![]()
![]() を部分分数に分ける場合,
を部分分数に分ける場合, ![]() として, 分子の係数比較を行い, 連立方程式などで, 定数
として, 分子の係数比較を行い, 連立方程式などで, 定数![]() の値を決めるといいでしょう。これも先と同様に, 分母をはらって恒等的な関係を用いる数値代入法で, 定数
の値を決めるといいでしょう。これも先と同様に, 分母をはらって恒等的な関係を用いる数値代入法で, 定数![]() が求まります。考え方自体は恒等式の攻め方と同じです。
が求まります。考え方自体は恒等式の攻め方と同じです。
【例】部分分数分解すると, ![]() となる。定数
となる。定数![]() の値を求めよ。
の値を求めよ。
【解法1】係数比較
右辺を通分すると, ![]()
これが左辺と等しいので, ![]()
これより, ![]() となる。これを解いて,
となる。これを解いて, ![]() となる。
となる。
※通分でなくとも, 両辺に![]() をかけて行ってもよい。
をかけて行ってもよい。
【解法2】数値代入法
両辺に![]() をかけて,
をかけて, ![]()
![]() のとき,
のとき, ![]()
![]() のとき,
のとき, ![]()
![]() のとき,
のとき, ![]()
![]() から,
から, ![]() これと
これと![]() を,
を, ![]() に代入し,
に代入し, ![]() から,
から, ![]()
以上より, ![]()
部分分数のつくり方は![]()
![]() は
は![]() より低次数。
より低次数。![]() は
は![]() より低次数と設定するのが一般的であると思われそうだが,
より低次数と設定するのが一般的であると思われそうだが, ![]() や
や![]() をそのやり方で設定してもうまくいかない場合がある。つまり,
をそのやり方で設定してもうまくいかない場合がある。つまり, ![]() や
や![]() の作り方を知らないと無限ループに落ちいることになる。
の作り方を知らないと無限ループに落ちいることになる。
このルールにしたがって, 上のパターン2の解法で, 部分分数をつくるとき, 次のように設定するとする。![]()
このとき, 【解法1】の係数比較の解法では, 未知数の文字が4つ![]() あるのに, 方程式が3つしか作れず,手詰まりとなる。しかし, 数値代入法を取り入れることで, 方程式は4つ以上作れるので, 問題なく答えられと考えるが, 無限ループにはまる。実際にやってみると, 次のようだ。
あるのに, 方程式が3つしか作れず,手詰まりとなる。しかし, 数値代入法を取り入れることで, 方程式は4つ以上作れるので, 問題なく答えられと考えるが, 無限ループにはまる。実際にやってみると, 次のようだ。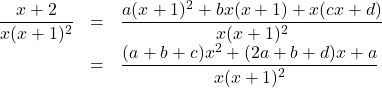
分子の係数比較より, ![]() ,
,
また, 分子だけの等式, ![]() に,
に, ![]() を代入すると,
を代入すると, ![]() となり,
となり, ![]() を
を![]() に代入すると,
に代入すると, ![]() ,
, ![]() ,
, ![]()
![]() より得られる式は,
より得られる式は, ![]() となり, これは
となり, これは![]() と同じである。
と同じである。
この後いくらやっても同じことになる。初めから数値代入法でやっても同じである。
したがって, ある程度部分分数の構成を知っておかないと, ドツボにはまることになる。
例えば, ![]() は
は![]() と分解する。しかし, この分解においても,
と分解する。しかし, この分解においても, ![]() としてしまうと, 今示したような無限ループにはまる。そもそも前途したパターン2の解法で, 分子を
としてしまうと, 今示したような無限ループにはまる。そもそも前途したパターン2の解法で, 分子を![]() としたことや, 今のように分子を
としたことや, 今のように分子を![]() としてなぜいけないのか。以下に示しました。
としてなぜいけないのか。以下に示しました。
そもそも間違いなのは, ![]() の式の部分数分解で, 分子を
の式の部分数分解で, 分子を![]() や
や![]() というようにおけないのである。理由は具体例を挙げると,
というようにおけないのである。理由は具体例を挙げると, ![]() を部分分数分解するとき, 次のように行うからである。
を部分分数分解するとき, 次のように行うからである。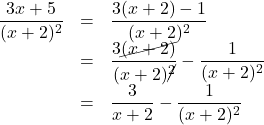
このように, 分子は必ず定数になるからである。
文字でやってみると, 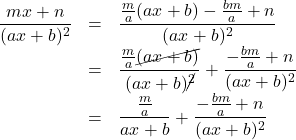
やはり, 分子に![]() を含む項は現れない。
を含む項は現れない。
だから, この場合の部分分数分解で, 分子を![]() などとおくことは失敗の原因になる。特に分母が因数分解できるときは気をつけた方がいい。
などとおくことは失敗の原因になる。特に分母が因数分解できるときは気をつけた方がいい。
一般的に分母の![]() や
や![]() の
の![]() の係数
の係数![]() は1であることが多いので, それで以下に部分分数分解のパターンを書いておく。これらの構成は知っておかないと, 先のようにドツボにはまる。
は1であることが多いので, それで以下に部分分数分解のパターンを書いておく。これらの構成は知っておかないと, 先のようにドツボにはまる。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
分子が1の場合の公式はこちらにまとめました。
 高校数学:分子が1の部分分数分解の求め方
高校数学:分子が1の部分分数分解の求め方![]() 分解した分数式の分子の定数を決める方法として, 係数比較と数値代入法がある。
分解した分数式の分子の定数を決める方法として, 係数比較と数値代入法がある。![]() 係数比較が面倒なときは, 数値代入法を使っていくとよい。
係数比較が面倒なときは, 数値代入法を使っていくとよい。![]() 分解した分数式を
分解した分数式を![]() とすると,
とすると, ![]() は
は![]() より低次数で, 一般的には
より低次数で, 一般的には![]() より次数を1つ下げるが, それでうまくいくとは限らない。きちんと部分分数分解の式の構成を把握しておくことが大事。
より次数を1つ下げるが, それでうまくいくとは限らない。きちんと部分分数分解の式の構成を把握しておくことが大事。
 数樂管理人のブログ
数樂管理人のブログ 

