こんにちは。今回は無限等比級数の収束と発散について書いておきます。
無限等比級数とは![]() を無限等比級数という。
を無限等比級数という。![]() は初項,
は初項, ![]() は公比
は公比
無限等比級数![]() において,
において, ![]() のとき, 収束して和は0
のとき, 収束して和は0![]() のとき,
のとき, ![]() なら, 収束して和は
なら, 収束して和は![]()
![]() ,
, ![]() なら, 発散する。
なら, 発散する。
【例】次の無限等比級数の収束, 発散を調べよ。
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
【解答例】
(1) ![]() (公比
(公比![]() )
)
したがって, 公比![]() が
が![]() より,
より, ![]() なので, これは収束する。
なので, これは収束する。
つまり, 初項![]() , 公比
, 公比![]() の無限等比級数である。
の無限等比級数である。
よって, 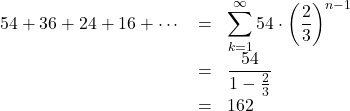
![]() (答)
(答)
(2) ![]() (公比
(公比![]() )
)
したがって, 公比![]() が
が![]() より,
より, ![]() なので発散する。
なので発散する。
発散する。![]() (答)
(答)
(3) ![]() (公比
(公比![]() )
)
したがって, 公比![]() が
が![]() より,
より, ![]() なので発散する。
なので発散する。
発散する。![]() (答)
(答)
(4) ![]() (公比
(公比![]() )
)
したがって, 公比![]() が
が![]() より,
より, ![]() なので, これは収束する。
なので, これは収束する。
つまり, 初項![]() , 公比
, 公比![]() の無限等比級数である。
の無限等比級数である。
よって, 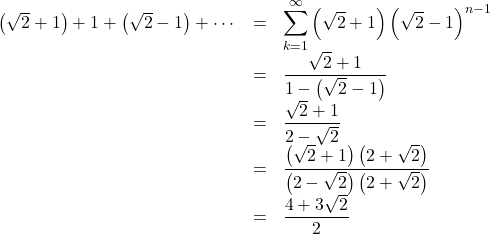
![]() (答)
(答)
 数樂管理人のブログ
数樂管理人のブログ 

