こんにちは。今回は変曲点とグラフの凹凸について書いておきます。
関数![]() の増減は, 導関数
の増減は, 導関数![]() の符号を用いて調べることができる。これと同じように考えると,
の符号を用いて調べることができる。これと同じように考えると, ![]() の増減は
の増減は![]() の導関数
の導関数![]() (
(![]() の第2次導関数)の符号で判定できる。
の第2次導関数)の符号で判定できる。![]() となる区間では,
となる区間では, ![]() は減少する。
は減少する。
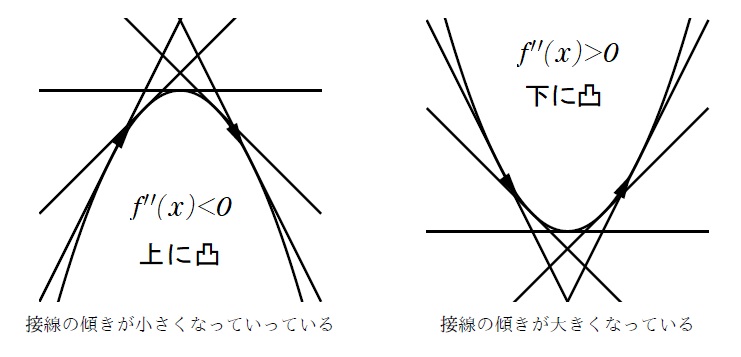
つまり, 関数![]() の接線の傾きは,
の接線の傾きは, ![]() の増加とともに小さくなっていくことを意味し, 関数
の増加とともに小さくなっていくことを意味し, 関数![]() はその区間で上に凸である。
はその区間で上に凸である。![]() となる区間では,
となる区間では, ![]() は増加する。
は増加する。
つまり, 関数![]() の接線の傾きは,
の接線の傾きは, ![]() の増加とともに大きくなっていくことを意味し, 関数
の増加とともに大きくなっていくことを意味し, 関数![]() はその区間で下に凸である。
はその区間で下に凸である。
関数![]() のある
のある![]() の値
の値![]() において,
において, ![]() が成り立ち,
が成り立ち, ![]() の前後で
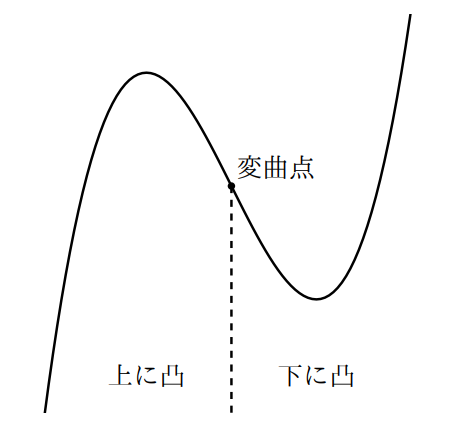
の前後で![]() の符号が変わるとき, 点
の符号が変わるとき, 点![]() は関数
は関数![]() の凹凸の変わり目であるといえる。この点を関数
の凹凸の変わり目であるといえる。この点を関数![]() の変曲点という。
の変曲点という。
ただし, ![]() であっても,
であっても, ![]() の前後で
の前後で![]() の符号に変化のないものは, 点
の符号に変化のないものは, 点![]() を変曲点としない。
を変曲点としない。
例:![]()
 emath:高校数学:3次関数の変曲点について
emath:高校数学:3次関数の変曲点について 数樂管理人のブログ
数樂管理人のブログ