こんにちは。今回は指数関数のところで, ![]() とおくとき, しておかなくてはならないことを書いておきます。当たり前のことなのですが, 忘れがちだったり, 範囲の求め方があいまいだったりするので書き留めておきます。問題を解きながら流れを見ていきましょう。
とおくとき, しておかなくてはならないことを書いておきます。当たり前のことなのですが, 忘れがちだったり, 範囲の求め方があいまいだったりするので書き留めておきます。問題を解きながら流れを見ていきましょう。
【問題】関数![]() の最小値を求めよ。
の最小値を求めよ。
(1) ![]() とおくとき,
とおくとき, ![]() の範囲を求めよ。
の範囲を求めよ。
(2) (1)のとき関数の最小値を求めよ。
【解答例】
(1) ![]() ,
, ![]() なので, 相加相乗平均を用いて,
なので, 相加相乗平均を用いて, ![]()
等号成立は, ![]() , つまり,
, つまり, ![]() のとき,
のとき,
よって, ![]() (答)
(答)
(2) 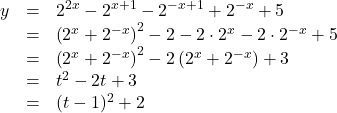
![]() より,
より, ![]() つまり,
つまり, ![]() のとき, 最小値3をる。
のとき, 最小値3をる。![]() (答)
(答)
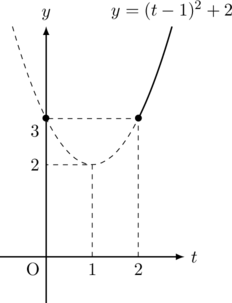
解法のコツ
![]() とおくときなどは,
とおくときなどは, ![]() ,
, ![]() から, 相加相乗平均を用いて,
から, 相加相乗平均を用いて, ![]() のとる範囲を定義することを忘れないように留意すること。
のとる範囲を定義することを忘れないように留意すること。
 数樂管理人のブログ
数樂管理人のブログ 


