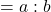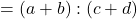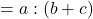こんにちは。台形に関する面積比の公式の紹介です。それではどうぞ。
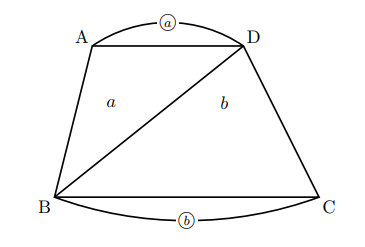
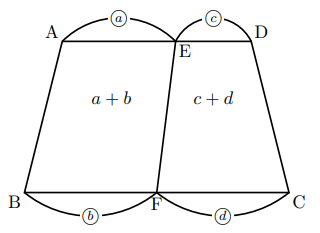
上底と下底の比が![]() の台形ABCDにおいて, 対角線BDで区切った△ABDと△DBCの面積比は,
の台形ABCDにおいて, 対角線BDで区切った△ABDと△DBCの面積比は, ![]() となる。これは, 台形の上底と下底は平行であるから, 2つの三角形の高さが等しいことになります。したがって, 底辺の長さの比がそのまま面積比になります。
となる。これは, 台形の上底と下底は平行であるから, 2つの三角形の高さが等しいことになります。したがって, 底辺の長さの比がそのまま面積比になります。
台形ABCDで, ![]() のとき, 台形ABFEと台形EFCDの面積比は
のとき, 台形ABFEと台形EFCDの面積比は![]() となります。これは2つの台形の高さが等しいので, 面積比が, (上底+下底)の比になるからです。
となります。これは2つの台形の高さが等しいので, 面積比が, (上底+下底)の比になるからです。
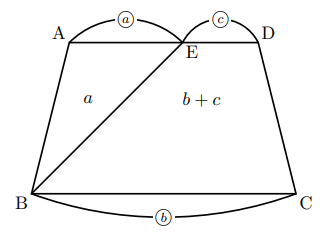
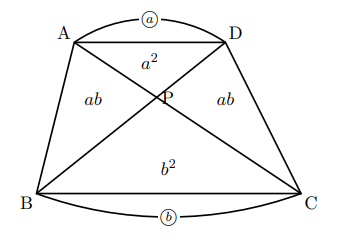
台形ABCDで, ![]() のとき, △ABEと台形EBCDの面積比は,
のとき, △ABEと台形EBCDの面積比は, ![]() になります。これも台形の上底と下底が平行なので, △ABEと台形EBCDの高さが等しいので, 面積比は, (上底+下底)の比になります。三角形は上底が0の台形と考えると,
になります。これも台形の上底と下底が平行なので, △ABEと台形EBCDの高さが等しいので, 面積比は, (上底+下底)の比になります。三角形は上底が0の台形と考えると, ![]() となり, 公式が得られます。
となり, 公式が得られます。
上底と下底の比が![]() の台形ABCDを, 2つの対角線AC, BDで, 三角形4つに分けます。このとき, 対角線の交点をPとすると, AD
の台形ABCDを, 2つの対角線AC, BDで, 三角形4つに分けます。このとき, 対角線の交点をPとすると, AD![]() BCから, △ADP∽△CBPが言え, それぞれの三角形の面積の割合は以下の図のようになります。
BCから, △ADP∽△CBPが言え, それぞれの三角形の面積の割合は以下の図のようになります。
△ADPと△CBPの![]() ,
, ![]() は相似比の2乗からきています。△ABPと△DCPの
は相似比の2乗からきています。△ABPと△DCPの![]() は,
は, ![]() であるから, △ADP:△ABP
であるから, △ADP:△ABP![]() からきています。△DCPも同様です。
からきています。△DCPも同様です。
 数樂管理人のブログ
数樂管理人のブログ