こんにちは。今回は座標軸上の線分比, 面積比について書いておきます。
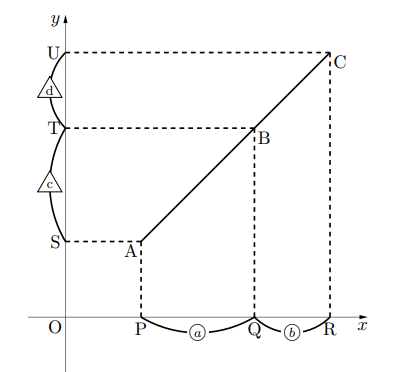
座標軸上の線分ACを点Bで分けるとき, ![]() (
(![]() 軸方向で見た場合)または,
軸方向で見た場合)または, ![]() (
(![]() 軸方向で見た場合)となります。
軸方向で見た場合)となります。
ちなみに![]() ですので, どちらの方向から見ても比(比の値)は同じになります。
ですので, どちらの方向から見ても比(比の値)は同じになります。
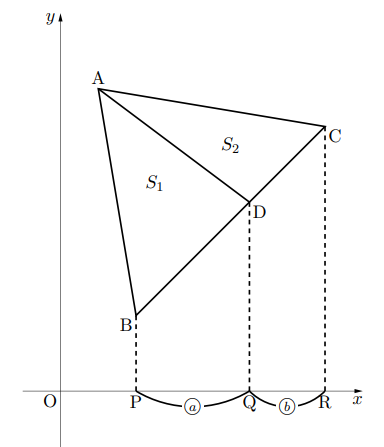
△ABDの面積を![]() , △ADCの面積を
, △ADCの面積を![]() とすると, この2つの三角形は, 底辺をそれぞれBD, DCとすると, 高さが等しいので, 面積比は底辺の比に比例します。ここで,
とすると, この2つの三角形は, 底辺をそれぞれBD, DCとすると, 高さが等しいので, 面積比は底辺の比に比例します。ここで, ![]() なので,
なので, ![]()
となります。
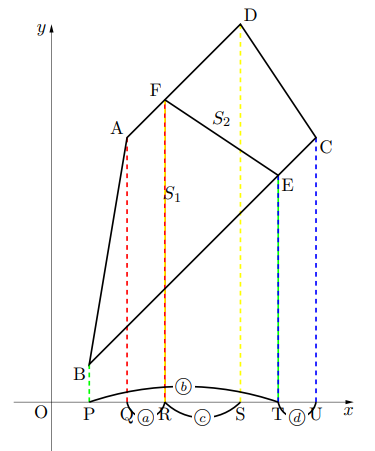
四角形ABCDは台形(平行四辺形でもよい)で四角形ABEFと四角形FECDはともに高さの等しい台形です。![]() とし, 四角形ABEFと四角形FECDの面積をそれぞれ,
とし, 四角形ABEFと四角形FECDの面積をそれぞれ, ![]() とすると, その面積比は, (上底+下底)の比(高さが等しいから)になるので,
とすると, その面積比は, (上底+下底)の比(高さが等しいから)になるので, ![]()
となります。
なんでかなぁって思う人は下の関連記事をたどってください。
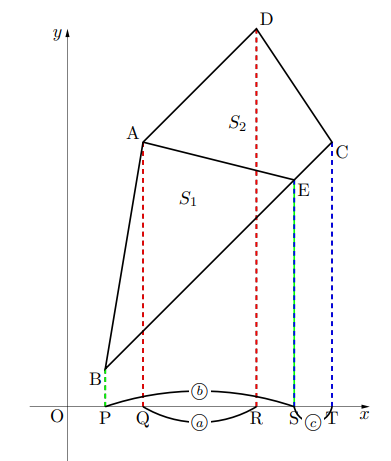
四角形ABCDは台形(平行四辺形でもよい)で, 線分AEでそれぞれ高さの等しい△ABEと台形AECDに分けます。![]() とし, △ABEと台形AECDの面積をそれぞれ,
とし, △ABEと台形AECDの面積をそれぞれ, ![]() とすると, その面積比は,
とすると, その面積比は, ![]()
となります。
理由は上の台形の面積比で片方の台形の上底を0とすれば, この公式と同様の式が得られます。
なんでかなぁって思う人は下の関連記事をたどってください。
 emath:中学数学:公式:攻略法:台形と面積比
emath:中学数学:公式:攻略法:台形と面積比 数樂管理人のブログ
数樂管理人のブログ