こんにちは。楕円の切り取る線分の長さに関する問題です。解法のテクニックとしてご覧ください。
直線![]() (
(![]() は実数)と, 楕円
は実数)と, 楕円![]() について次の問いに答えよ。
について次の問いに答えよ。
(1) 両者が異なる2点で交わるための条件を求めよ。
(2) 2つの交点を結ぶ線分の長さが4となるとき, ![]() の値を求めよ。
の値を求めよ。
【岩手大】
【方針】
(1)は直線の式を楕円の式に代入して判別式![]() で完遂。
で完遂。
(2)は交点の座標のおき方に注意して解と係数の関係を用いて解く(頻出解法)
【解答例】
(1) ![]() を
を![]() に代入すると,
に代入すると, ![]()
![]()
![]() が異なる2つの実数解をもてばよいので,
が異なる2つの実数解をもてばよいので,
判別式![]() とすると,
とすると, ![]() だから,
だから, ![]()
![]()
![]()
![]()
![]() (答)
(答)
(2) 交点の座標を![]() ,
, ![]() とおく,
とおく,
(※楕円の式の方で座標設定するととんでもないことになるので注意)![]() なので,
なので, 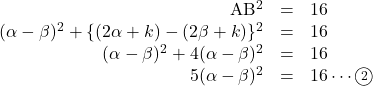
![]() は
は![]() の解なので, 解と係数の関係より,
の解なので, 解と係数の関係より, ![]() ,
, ![]()
ここで, ![]() を変形すると,
を変形すると, ![]() となり,
となり, ![]() らを代入すると,
らを代入すると, 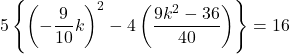
![]()
![]()
![]()
![]() (答)
(答)
 数樂管理人のブログ
数樂管理人のブログ 

