こんにちは。今回は積の微分の公式のなぜを示したいと思います。それではいってみましょう。
積の微分の公式
積の微分の公式とは以下のようなものである。![]()
3つの積の微分の場合は![]()
となる。
例えば, ![]() を微分すると,
を微分すると, 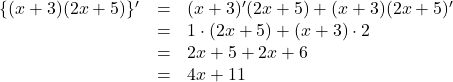
![]() を微分すると,
を微分すると, 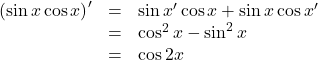
![]() を微分すると,
を微分すると, 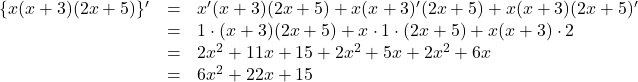
このような微分の方法のことをいう。
以下になぜそうなるか導いてみた。1行目から2行目への工夫の仕方を学んでほしい。![]() として, 導関数の定義にしたがって微分すると,
として, 導関数の定義にしたがって微分すると, 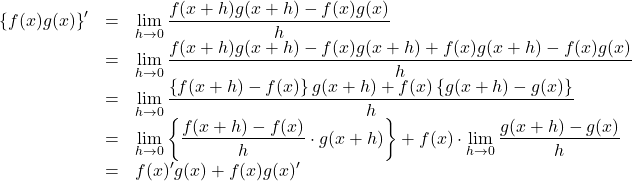
以上より, ![]()
が成り立つ。
![]() とするとき,
とするとき, ![]() とすると,
とすると, ![]() となり, これを先の公式にしたがって微分すると,
となり, これを先の公式にしたがって微分すると, ![]()
ここで, ![]() は,
は, ![]()
となる。![]() ,
, ![]() を
を![]() に代入して,
に代入して, ![]()
よって, ![]()
が成り立つ。
 数樂管理人のブログ
数樂管理人のブログ 

