高校数学：数III極限：lim[x→0] sinx/x=1のなぜ・グラフ付き

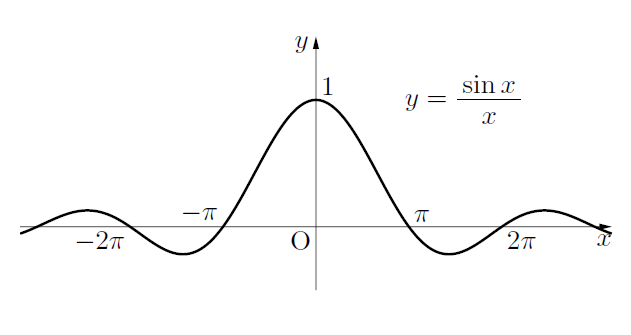
こんにちは。数IIIの極限のところで出てくる有名な公式です。これまた有名な証明方法で示していきましょう。最後にグラフの概形を載せています。

公式

$\displaystyle \lim_{x\to0}\dfrac{\sin x}{x}=1$

証明

以下の図形を用いて証明を行っていきます。それぞれの図形は,
$\bigtriangleup{\mathrm{OAC}}\cdots$ 頂角が $x$ , 2辺が1の二等辺三角形,
扇形 $\bigtriangleup{\mathrm{OAC}}\cdots$ 半径1,中心角 $x$ ,
$\bigtriangleup{\mathrm{OAB}}\cdots$ 直角を挟む2辺が, $1, \tan x$ の直角三角形
となっており, これらの大小関係を不等式で表して, 極限をとっていきます。

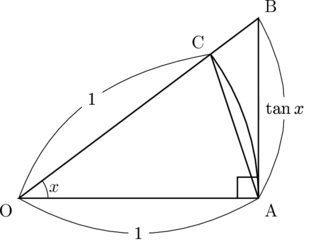
上の図において, 面積の関係から下の不等式が成立する。
$\bigtriangleup{\mathrm{OAC}}<$ 扇形 $\bigtriangleup{\mathrm{OAC}}<\bigtriangleup{\mathrm{OAB}}$
ここで, それぞれ面積を求めると,
$\bigtriangleup{\mathrm{OAC}}=\dfrac12\cdot1\cdot1\cdot\sin x=\dfrac12\sin x$
扇形 $\mathrm{OAC}=\dfrac12\cdot1^2\cdot x=\dfrac12 x$
$\bigtriangleup{\mathrm{OAB}}=\dfrac12\cdot1\cdot\tan x=\dfrac12\tan x$
よって, 先の不等式にこれらを代入すると,
$\dfrac12\sin x<\dfrac12 x<\dfrac12\tan x$
$\sin x<x<\tan x$
$\sin x< x <\dfrac{\sin x}{\cos x}$
辺々を $\sin x$ で割ると
$1<\dfrac{x}{\sin x}<\dfrac{1}{\cos x}$
辺々の逆数をとると,
$\cos x<\dfrac{\sin x}{x}<1$
ここで,
$\displaystyle\lim_{x\to+0}\cos x<\displaystyle\lim_{x\to+0}\dfrac{\sin x}{x}<1$
とすると,
$\displaystyle\lim_{x\to+0}\cos x=1$ なので, はさみうちの原理から,
$\displaystyle\lim_{x\to+0}\dfrac{\sin x}{x}=1$
また,
$\dfrac{\sin x}{x}=\dfrac{\sin(-x)}{-x}$ なので,
$\displaystyle\lim_{x\to-0}\dfrac{\sin x}{x}=1$
以上より,
$\displaystyle \lim_{x\to0}\dfrac{\sin x}{x}=1$
が成り立つ。