TikZ：少しでも頭に入れておきたいグラフたち(logx編)

こんにちは。数IIIやってると頻繁に出てくるグラフってあるんです。ですから, ある程度記憶しておくと便利かなと思って書いておきます。今回はその対数関数編です。

y=xlogx

$y=x\log x\ (x>0)$ のグラフ
$f(x)=x\log x$ とおくと,
$f'(x)=\log x+x\cdot x^{-1}=\log x+1$
$f''(x)=\dfrac{1}{x}>0$
$f'(x)=0$ とすると, $x=e^{-1}$ である。
これらをもとにグラフを描くと, 以下のようになる。

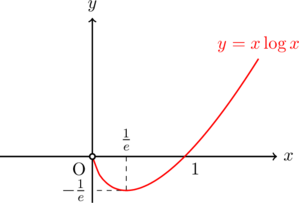
極値に関して
$x=\dfrac1e$ で極小値 $-\dfrac1e$ をとる。
極大値なし
変曲点なし
漸近線なし

y=logx/x

$y=\dfrac{\log x}{x}\ (x>0)$ のグラフ
$f(x)=\dfrac{\log x}{x}$ とおくと,
$f(x)=x^{-1}\log x$ なので,
$f'(x)=-x^{-2}\log x+x^{-1}\cdot x^{-1}=x^{-2}\left(-\log x+1\right)$
$f''(x)=-2x^{-3}\left(-\log x+1\right)+x^{-2}\cdot \left(-x^{-1}\right)=x^{-3}\left(2\log x-3\right)$
$f'(x)=0$ とすると, $x=e$ ,
$f''(x)=0$ とすると, $x=e^{\frac32}$ である。
これらをもとにグラフを描くと, 以下のようになる。

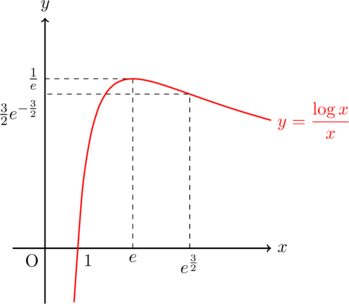
極値に関して
$x=e$ で極大値 $\dfrac1e$ をとる。
極小値なし
変曲点 $\left(e^{\frac32}, \dfrac32e^{-\frac32}\right)$
漸近線
$x=0$ ( $y$ 軸), $\displaystyle \lim_{x\to+0}\dfrac{\log x}{x}=-\infty$
$y=0$ ( $x$ 軸), $\displaystyle \lim_{x\to\infty}\dfrac{\log x}{x}=0$

y=logx/√x

$y=\dfrac{\log x}{\sqrt{x}}\ (x>0)$ のグラフ
$f(x)=\dfrac{\log x}{\sqrt{x}}$ とおくと,
$f(x)=x^{-\frac12}\log x$ なので,
$f'(x)=-\dfrac12 x^{-\frac32}\logx+x^{-\frac12}\cdot x^{-1}=\dfrac12x^{-\frac32}\left(-\log x+2\right)$
$f''(x)=-\dfrac32x^{-\frac52}\left(-\dfrac12\log x+1\right)+x^{-\frac32}\cdot \left(-\dfrac12x^{-1}\right)=-\dfrac14x^{-\frac52}\left(-3\log x+8\right)$
$f'(x)=0$ とすると, $x=e^2$
$f''(x)=0$ とすると, $x=e^{\frac83}$
これらをもとにグラフを描くと, 以下のようになる。(描画の都合上極値などが示せていない)

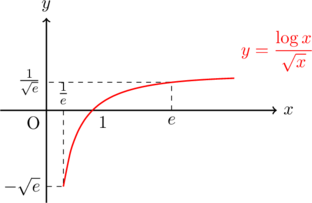
極値に関して
$x=e^2$ で極大値 $\dfrac2e$ をとる。
極小値なし
変曲点 $\left(e^{\frac83}, \dfrac83e^{-\frac43}\right)$
漸近線
$x=0$ ( $y$ 軸), $\displaystyle \lim_{x\to+0}\dfrac{\log x}{\sqrt{x}}=-\infty$
$y=0$ ( $x$ 軸), $\displaystyle \lim_{x\to\infty}\dfrac{\log x}{\sqrt{x}}=0$

y=(logx)²/x

$y=\dfrac{(\log x)^2}{x}\ (x>0)$ のグラフ
$f(x)=\dfrac{(\log x)^2}{x}$ とおくと,
$f(x)=x^{-1}(\log x)^2$ なので,
$f'(x)=-x^{-2}(\log x)^2+x^{-1}\cdot 2\log x\cdot x^{-1}=x^{-2}\log x(-\log x+2)$
$f''(x)$ は略
$f'(x)=0$ とすると, $x=1, e^2$
これらをもとにグラフを描くと, 以下のようになる。(描画の都合上極大値が示せていない)

極値に関して
$x=e^2$ で極大値 $\dfrac{4}{e^2}$ をとる。
$x=1$ で極小値0をとる。
変曲点はあるが特に覚えなくてよい。
漸近線
$x=0$ ( $y$ 軸), $\displaystyle \lim_{x\to+0}\dfrac{\left(\log x\right)^2}{x}=\infty$
$y=0$ ( $x$ 軸), $\displaystyle \lim_{x\to\infty}\dfrac{\left(\log x\right)^2}{x}=0$

y=(logx)²/√x

$y=\dfrac{(\log x)^2}{\sqrt{x}}\ (x>0)$ のグラフ
$f(x)=\dfrac{(\log x)^2}{\sqrt{x}}$ とおくと,
$f(x)=x^{-\frac12}(\log x)^2$ なので,
$f'(x)=-\dfrac12x^{-\frac32}(\log x)^2+x^{-\frac12}\cdot 2\log x\cdot x^{-1}=\dfrac12x^{-\frac32}\log x(-\log x+4)$
$f''(x)$ は略
$f'(x)=0$ とすると, $x=1, e^4$
これらをもとにグラフを描くと, 以下のようになる。(描画の都合上極大値が示せていない)

$x=e^4$ で極大値 $\dfrac{16}{e^2}$ をとる。
$x=1$ で極小値0をとる。
変曲点はあるが特に覚えなくてよい。
漸近線
$x=0$ ( $y$ 軸), $\displaystyle \lim_{x\to+0}\dfrac{\left(\log x\right)^2}{\sqrt{x}}=\infty$
$y=0$ ( $x$ 軸), $\displaystyle \lim_{x\to\infty}\dfrac{\left(\log x\right)^2}{\sqrt{x}}=0$

y=x/logx

$y=\dfrac{x}{\log x}\ (x>0)$ のグラフ
$f(x)=\dfrac{x}{\log x}$ とおくと,
$f(x)=x(\log x)^{-1}$ なので,
$f'(x)=(\log x)^{-1}+x\cdot -(\log x)^{-2}\cdot x^{-1}=(\log x)^{-1}\left\{1-(\log x)^{-1}\right\}$
$\begin{array}{lll}f''(x)&=&-(\log x)^{-2}\cdot x^{-1}\left\{1-(\log x)^{-1}\right\}+(\log x)^{-1}\left\{-(-1)\cdot(\log x)^{-2}\cdot x^{-1}\right\}\\&=&x^{-1}(\log x)^{-2}\left\{2(\log x)^{-1}-1\right\}\end{array}$
$f'(x)=0$ とすると, $x=e$
$f''(x)=0$ とすると, $x=e^2$
これらをもとにグラフを描くと, 以下のようになる。

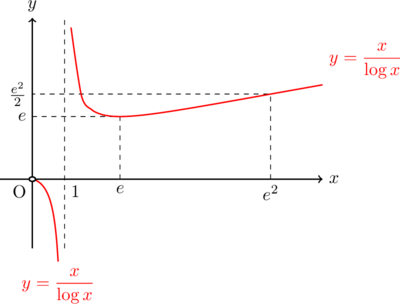
極値に関して
$x=e$ で極小値 $e$ をとる。
極大値はなし。
変曲点 $\left(e^2, \dfrac{e^2}{2}\right)$
漸近線
$x=1$
$\displaystyle \lim_{x\to1+0}\dfrac{x}{\log{x}}=\infty$
$\displaystyle \lim_{x\to1-0}\dfrac{x}{\log{x}}=-\infty$
ちなみに
$\displaystyle \lim_{x\to\infty}\dfrac{x}{\log{x}}=\infty$
$\displaystyle \lim_{x\to+0}\dfrac{x}{\log{x}}=0$