こんにちは。今回は数IIIで覚えておきたいグラフたちの指数関数編をやっていきます。グラフの概形関連づけて覚えておくと何かと便利です。それではどうぞ。
![]() のグラフ
のグラフ![]() とすると,
とすると, ![]()
![]()
![]() となるのは,
となるのは, ![]()
![]() となるのは,
となるのは, ![]()
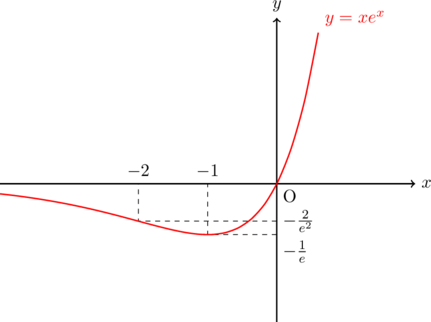
極値に関して
極大値なし
変曲点
漸近線
また,
![]() のグラフ
のグラフ![]() とすると,
とすると, ![]()
![]()
![]() となるのは,
となるのは, ![]() より,
より, ![]()
![]() となるのは,
となるのは, ![]() より,
より, ![]()
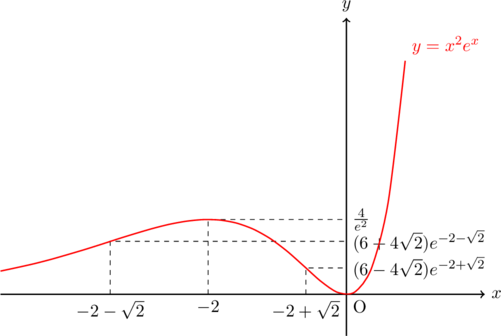
極値に関して
変曲点
漸近線
また,
![]() のグラフ
のグラフ![]() とおくと,
とおくと, ![]()
![]()
![]() となるのは,
となるのは, ![]()
![]() となるのは,
となるのは, ![]()
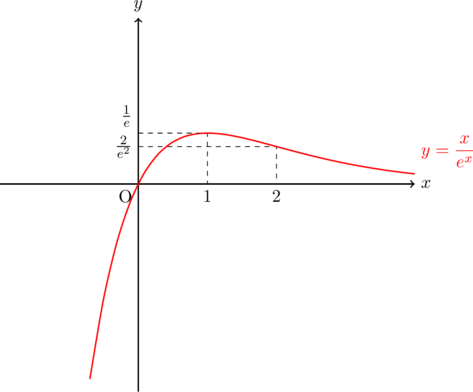
極値に関して
極小値なし
変曲点
漸近線
また,
こんにちは。今回は数IIIで覚えておきたいグラフたちの指数関数編をやっていきます。グラフの概形関連づけて覚えておくと何かと便利です。それではどうぞ。
![]() のグラフ
のグラフ![]() とすると,
とすると, ![]()
![]()
![]() となるのは,
となるのは, ![]()
![]() となるのは,
となるのは, ![]()

![]() のグラフ
のグラフ![]() とすると,
とすると, ![]()
![]()
![]() となるのは,
となるのは, ![]() より,
より, ![]()
![]() となるのは,
となるのは, ![]() より,
より, ![]()

![]() のグラフ
のグラフ![]() とおくと,
とおくと, ![]()
![]()
![]() となるのは,
となるのは, ![]()
![]() となるのは,
となるのは, ![]()
