こんにちは。数IIIでよく登場するサイクロイド曲線について書いておきます。
サイクロイドとは, ![]() ,
, ![]() とし, 媒介変数表示
とし, 媒介変数表示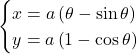
で表される曲線のことをいう。
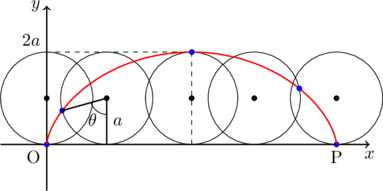
図形的な意味は, 直線に沿って, 半径![]() の円がちょうど1回転するときの円周上の1点(定点:図中青色)の軌跡を表している。したがって, 線分
の円がちょうど1回転するときの円周上の1点(定点:図中青色)の軌跡を表している。したがって, 線分![]() の長さは, 半径
の長さは, 半径![]() の円周の長さ
の円周の長さ![]() と一致する。
と一致する。
![]() を
を![]() で微分すると,
で微分すると, ![]() となる。
となる。![]() の範囲では,
の範囲では, ![]() なので,
なので, ![]() である。
である。
したがって, ![]() が増加すれば,
が増加すれば, ![]() の値も増加する。
の値も増加する。![]() を
を![]() で微分すると,
で微分すると, ![]() となる。
となる。![]() において,
において, ![]() は,
は, ![]() で
で![]() であるから,
であるから, ![]() で,
で, ![]() で
で![]() であるから,
であるから, ![]() である。
である。
したがって, ![]() の値は,
の値は, ![]() で増加し,
で増加し, ![]() で減少する。
で減少する。
これをもとにグラフを描くと以下のようになる。
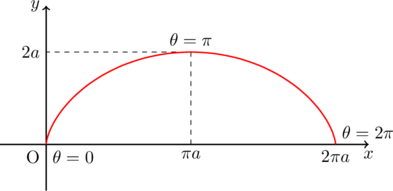
さてサイクロイドの弧の長さを求めていきましょう。
求める長さを![]() とすると,
とすると, ![]() ,
, ![]() であるから,
であるから, 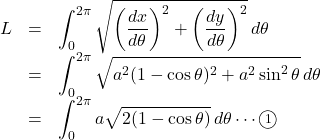
半角の公式より, ![]() であるから,
であるから, ![]() は次のようになる。
は次のようになる。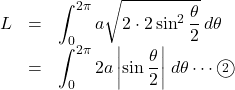
![]() より,
より, ![]() なので,
なので, ![]() である。
である。
よって, ![]() の絶対値はそのまま外せる。したがって,
の絶対値はそのまま外せる。したがって, ![]() を計算すると,
を計算すると, ![Rendered by QuickLaTeX.com \begin{array}{lll}L&=&\displaystyle\int_0^{2\pi}2a\sin\dfrac{\theta}{2}\, d\theta\\&=&2a\left[-2\cos\dfrac{\theta}{2}\right]_0^{2\pi}\\&=&2a\left\{2-(-2)\right\}\\&=&8a\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-dcfb17ff0a4a9867536218ad606bba89_l3.png)
よって曲線の長さは![]() となります。
となります。
サイクロイド曲線と![]() 軸で囲まれた面積を求めてみましょう。
軸で囲まれた面積を求めてみましょう。
求める面積を![]() とすると,
とすると, 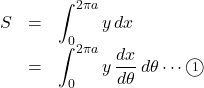
として求めていきます。![]() で,
で, ![]() が
が![]() となるとき,
となるとき, ![]() は
は![]() となるので,
となるので, ![]() は次のように計算できる。
は次のように計算できる。![Rendered by QuickLaTeX.com \begin{array}{lll}S&=&\displaystyle\int_0^{2\pi}a\left(1-\cos\theta\right)\cdota\left(1-\cos\theta\right)\,d\theta\\&=&a^2\displaystyle\int_0^{2\pi}\left(1-2\cos\theta+\cos^2\theta\right)\, d\theta\\&=&a^2\displaystyle\int_0^{2\pi}\left(1-2\cos\theta+\dfrac{1+\cos2\theta}{2}\right)\,d\theta\\&=&a^2\displaystyle\int_0^{2\pi}\left(\dfrac32-2\cos\theta+\dfrac{\cos2\theta}{2}\right)\,d\theta\\&=&a^2\left[\dfrac32\theta-2\sin\theta+\dfrac{\sin2\theta}{4}\right]_0^{2\pi}\\&=&a^2\left\{\left(3\pi-0+0\right)-\left(0-0+0\right)\right\}\\&=&3\pi a^2\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-0b4ac5961b5efab843b26c7fc131be02_l3.png)
よって, 面積は![]() になる。
になる。
※計算途中, 倍角の公式より, ![]()
としている。
上で求めた面積を![]() 軸を回転の軸として1回転させたときにでいる立体の体積を求めてみる。
軸を回転の軸として1回転させたときにでいる立体の体積を求めてみる。
求める体積を![]() とすると,
とすると, 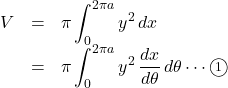
として求めていきます。![]() で,
で, ![]() が
が![]() となるとき,
となるとき, ![]() は
は![]() となるので,
となるので, ![]() は次のように計算できる。
は次のように計算できる。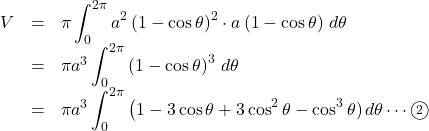
ここで, 倍角の公式と3倍角の公式より, ![]()
![]()
を用いて, ![]() を書き換えると,
を書き換えると, ![Rendered by QuickLaTeX.com \begin{array}{lll}V&=&\pi a^3\displaystyle\int_0^{2\pi}\left(\dfrac52-\dfrac{15}{2}+\dfrac32\cos2\theta-\dfrac14\cos3\theta\right)\,d\theta\\&=&\pi a^3\left[\dfrac52\theta-\dfrac{15}{4}\sin\theta+\dfrac34\sin2\theta-\dfrac{1}{12}\sin3\theta\right]_0^{2\pi}\\&=&\pi a^3\left\{\left(5\pi-0+0-0\right)-\left(0-0+0-0\right)\right\}\\&=&5\pi^2 a^3\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-97f149276e3ff861dc8e961b32cd07f2_l3.png)
よって, 体積は![]() になる。
になる。
サイクロイド曲線![]() ,
, ![]()
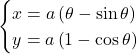
について。![]() サイクロイドの曲線の長さは,
サイクロイドの曲線の長さは, ![]()
![]() 曲線と
曲線と![]() 軸で囲まれた面積は,
軸で囲まれた面積は, ![]()
![]()
![]() の図形を
の図形を![]() 軸について1回転させてできる体積は,
軸について1回転させてできる体積は, ![]()
 数樂管理人のブログ
数樂管理人のブログ 


曲線の長さでL=∫[0→2π]2asinθ/2 dθ で =2a[-2cosθ/2][0→2π] は納得ですが どうしてそれが=2a(2-(-2))となるのかわかりません。その理由を教えてください。
失礼ですが、
三角関数の計算はされたことありますか?
積分計算はされたことありますか?
積分計算そのものです。
ですからそうなります。
ちなみにcosπ=-1,cos0=1です。
よろしくお願いします。