今回は![]() のグラフについて書いておきます。関数を見たらグラフの概形が浮かぶ。そんな具合になるまで練習を積んでください。
のグラフについて書いておきます。関数を見たらグラフの概形が浮かぶ。そんな具合になるまで練習を積んでください。
![]()
この関数は, ![]() ,
, ![]() で定義されます。
で定義されます。
これを変形すると, ![]() となり, この両辺を2乗すると,
となり, この両辺を2乗すると, ![]() とおく,
とおく, ![]() の両辺を
の両辺を![]() で微分すると,
で微分すると, ![]()
これは, ![]() のとき,
のとき, ![]() であるから,
であるから, ![]() は単調減少。
は単調減少。
また, ![]() で
で![]() となり,
となり, ![]() ,
, ![]() である。
である。![]() もこれを満たす。
もこれを満たす。![]() の
の![]() を入れ換えても式は変わらないので, この曲線は
を入れ換えても式は変わらないので, この曲線は![]() について対称である。
について対称である。
以上のことからグラフを描くと以下の赤線部のようになる。
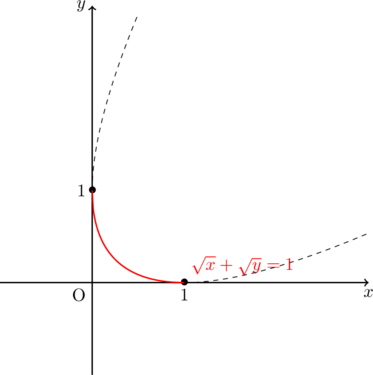
![]() の一般形として,
の一般形として, ![]() としても, 同様のグラフが得られる。このとき,
としても, 同様のグラフが得られる。このとき, ![]() 軸,
軸, ![]() 軸の交点がそれぞれ,
軸の交点がそれぞれ, ![]() ,
, ![]() となる。
となる。
また, この曲線はアステロイドに似ているが, この曲線は放物線の一部になる(証明割愛)。グラフ中の破線部は放物線の概形を記したものである。
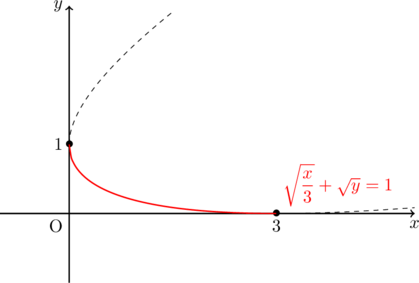
【出題例】東北大では以下の関数が問題文の中にあった。![]() ,
, ![]()
グラフは以下の赤線部ようになる。もちろん, こちらも放物線の一部になる。
 数樂管理人のブログ
数樂管理人のブログ 

