TikZ：高校数学：図形と方程式：3本の直線が三角形を作らない場合

2023年5月20日2023年5月21日

SHARE

こんにちは。この問題は初見で詰まりませんでしたか？定期テストにはよく出てくるかもしれません。それではどうぞ。

問題

【問題】3つの直線 $\ell:2x+y=5$ , $m:-x+y=-1$ , $n:ax+(a-1)y=-7$ が三角形を作らないとき, 定数 $a$ の値を求めよ。

解答例

【解答例】

3本の直線 $\ell, m, n$ が三角形を作らないということは, 以下の3通りの場合が考えられる。
【パターン1】3本の直線 $\ell, m, n$ が1点で交わるとき(下図イメージ図)

【パターン2】2本の直線 $\ell, n$ が平行になる場合(下図イメージ図)

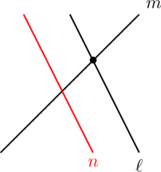
【パターン3】2本の直線 $m, n$ が平行になる場合(下図イメージ図)

それでは解いていきましょう。
【パターン1】
直線 $\ell, m$ の交点を求めると, $( 2, 1 )$ なので, 直線 $n$ にこれを代入して $a$ の値を求めるとよい。
よって,
$2a+(a-1)=-7$
$3a=-6$
$a=-2$
【パターン2】
直線 $n$ の傾きを求める。
$(a-1)y=-ax-7$ より, 直線 $n$ の傾きは $-\dfrac{a}{a-1}$ 。
これが直線 $\ell$ の傾きと一致すればよい。直線 $\ell$ の傾きは $-2$ なので,
$-\dfrac{a}{a-1}=-2$
$a=2(a-1)$
$a=2$
【パターン3】
パターン2より, 直線 $\ell$ の傾きは $-\dfrac{a}{a-1}$ , 直線 $m$ の傾きは1なので, この2つの傾きが一致すればよい。
したがって,
$-\dfrac{a}{a-1}=1$
$-a=a-1$
$a=\dfrac12$
以上より求める定数 $a$ の値は,
$a=-2, 2, \dfrac12\cdots$ (答)

コメントを残すコメントをキャンセル

前の記事

高校数学：常用対数：桁数と最高位の数を求める

次の記事

TikZ：令和4年度中2徳島県基礎学力テスト(大問5平面図形)