こんにちは。微分の定義についての問題です。それではどうぞ。
【問題】次の会話文を読んで【 】の中を適当な語句や式で埋めなさい。【![]() 】は途中の計算式も書くこと。
】は途中の計算式も書くこと。
A:微分係数って何ですか?
B:微分係数の定義を考えてみると, 関数![]() 上の
上の![]() の値が
の値が![]() から
から![]() に変化するときの平均変化率【
に変化するときの平均変化率【![]() 】において,
】において, ![]() を限りなく
を限りなく![]() に近づけたときの値を言うので, 【
に近づけたときの値を言うので, 【![]() 】と書けます。この値を関数
】と書けます。この値を関数![]() の点
の点![]() における微分係数と言い,
における微分係数と言い, ![]() と表します。また, 【
と表します。また, 【![]() 】の式で,
】の式で, ![]() とおくと,
とおくと, ![]() のとき,
のとき, ![]() となり, 【
となり, 【![]() 】の式を書き換えると,
】の式を書き換えると, ![]() となります。これらが微分係数
となります。これらが微分係数![]() の定義です。
の定義です。
A:平均変化率って, 直線の【![]() 】と同じ意味をもちますね。
】と同じ意味をもちますね。
B:そう。だから![]() は関数
は関数![]() の点
の点![]() における【
における【![]() 】の傾きを表すことになるんだ。
】の傾きを表すことになるんだ。
A:そうなんですね。それでは, ![]() の
の![]() における微分係数を, 微分係数の定義にしたがって求めると, 【
における微分係数を, 微分係数の定義にしたがって求めると, 【![]() 】となりますね。
】となりますね。
B:一般に![]() を微分すると, 【
を微分すると, 【![]() 】となることが知られています。
】となることが知られています。
【解答例】
【![]() 】
】![]()
【![]() 】
】![]()
【![]() 】傾き
】傾き
【![]() 】接線
】接線
【![]() 】
】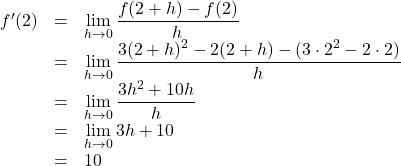
【![]() 】
】![]()
 数樂管理人のブログ
数樂管理人のブログ 


