TikZ：高校数学：三角比：sin²θ＋cos²θ＝1の証明とその周辺の暗記

2023年6月8日2023年6月18日

こんにちは。 $\sin^2\theta+\cos^2\theta=1$ の証明と, その周辺の暗記を書いておきます。

sin²θ＋cos²θ＝1

直角三角形ABCの斜辺の長さを $\mathrm{AB}=1$ , $\kaku{ABC}=\theta$ とすると, $\mathrm{BC}=\cos\theta$ , $\mathrm{CA}=\sin\theta$ となる。
図1

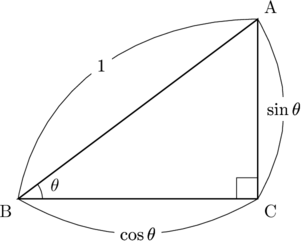
これに三平方の定理を用いると,
$\sin^2\theta+\cos^2\theta=1$
が成り立ちます。

先ほどの図1で3つの辺すべて $\cos\theta(\cos\theta\neq0)$ で割ると, 図2となる。
図2

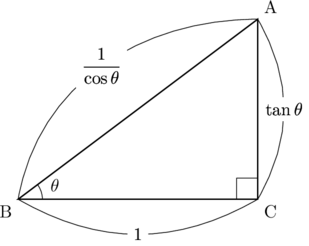
これに三平方の定理を用いると,
$1+\tan^2\theta=\dfrac{1}{\cos^2\theta}$
が成り立ちます。

先ほどの図1で3つの辺すべて $\sin\theta(\sin\theta\neq0)$ で割ると, 図3となる。
図3

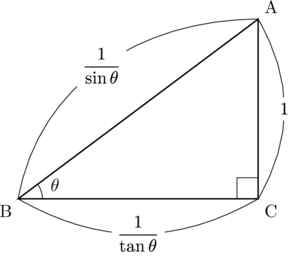
これに三平方の定理を用いると,
$1+\dfrac{1}{\tan^2\theta}=\dfrac{1}{\sin^2\theta}$
が成り立ちます。

これとは別の証明は以下の記事を参照ください。