こんにちは。いろいろ勉強して覚えたことです。忘備録として書いておきます。意外と覚えやすい証明方法ですので, ご参考にしてください。
斜辺ABの長さが1の直角三角形AEBがあり, それが図のように台形ABCDにちょうど収まっているとする。点Eは辺CD上にある。また, ![]() ,
, ![]() ,
, ![]() とする。
とする。
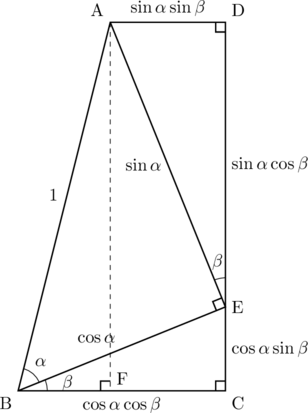
このとき,
ここで, 図のように, 点Aから下底へ垂線AFを引くと, 直角三角形ABFができる。このとき,
これより,
が得られる。
が得られる。
最後に,
これまでの証明を利用すると,
右辺の分子分母を
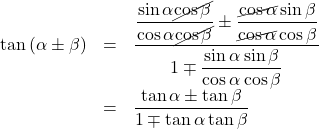
以上より,
このような感じで加法定理が証明できる。
案外覚えやすいので, 覚えられるなら覚えておいた方がいいと思う。
加法定理
![]()
![]()
![]()
![]()
![]()
![]()
 数樂管理人のブログ
数樂管理人のブログ 

