こんにちは。対数の処理の問題です。慣れてない人はその試行を覚えておくといいですよ。
【問題】![]() を正の実数とする。以下の問いに答えよ。
を正の実数とする。以下の問いに答えよ。
(1) ![]() を
を![]() のみの式で表せ。
のみの式で表せ。
(2) ![]() を簡単にせよ。
を簡単にせよ。
(3) 方程式![]() を満たす実数
を満たす実数![]() を求めよ。
を求めよ。
【東北学院大学】
【解答例】
(1) ![]() とおく。
とおく。
両辺を底が![]() の対数をとると
の対数をとると![]()
よって, ![]()
![]() (答)
(答)
(2) ![]() とおく。
とおく。
両辺を底が2の対数をとると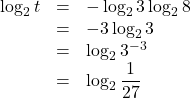
よって![]()
![]() (答)
(答)
(3) (2)より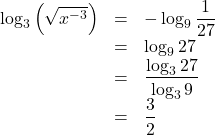
この式の意味から, ![]()
両辺2乗して![]()
![]()
![]() より,
より, ![]() (答)
(答)
こんにちは。対数の処理の問題です。慣れてない人はその試行を覚えておくといいですよ。
【問題】![]() を正の実数とする。以下の問いに答えよ。
を正の実数とする。以下の問いに答えよ。
(1) ![]() を
を![]() のみの式で表せ。
のみの式で表せ。
(2) ![]() を簡単にせよ。
を簡単にせよ。
(3) 方程式![]() を満たす実数
を満たす実数![]() を求めよ。
を求めよ。
【東北学院大学】
【解答例】
(1) ![]() とおく。
とおく。
両辺を底が![]() の対数をとると
の対数をとると![]()
よって, ![]()
![]() (答)
(答)
(2) ![]() とおく。
とおく。
両辺を底が2の対数をとると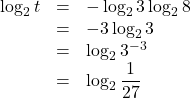
よって![]()
![]() (答)
(答)
(3) (2)より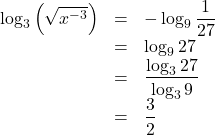
この式の意味から, ![]()
両辺2乗して![]()
![]()
![]() より,
より, ![]() (答)
(答)