高校数学：期待値：確率と期待値(佐賀大学)

2023年11月5日

この問題は取り組みやすいかもしれません。それではやってみましょう。

佐賀大学

【問題】袋の中に赤玉3個, 白玉2個, 黒玉1個が入っている。この袋から2個の玉を同時に取り出す。このとき, 赤玉1個につき1点, 白玉1個につき2点, 黒玉1個につき3点もらえる。もらえる合計点の期待値を求めよ。
【佐賀大学】

解答・解説

【解答】 $\dfrac{10}{3}$ (点)
【解説】
玉の取り出し方と確率を調べると,
すべての取り出し方は, $_6\mathrm{C}_2=15$ 通り。
(赤, 赤)　2点, 確率　 $\dfrac{_3\mathrm{C}_2}{15}=\dfrac{3}{15}$
(赤, 白)　3点, 確率　 $\dfrac{_3\mathrm{C}_1\cdot_2\mathrm{C}_1}{15}=\dfrac{6}{15}$
(赤, 黒)　4点, 確率　 $\dfrac{_3\mathrm{C}_1\cdot_1\mathrm{C}_1}{15}=\dfrac{3}{15}$
(白, 白)　4点, 確率　 $\dfrac{_2\mathrm{C}_2}{15}=\dfrac{1}{15}$
(白, 黒)　5点, 確率　 $\dfrac{_2\mathrm{C}_1\cdot_1\mathrm{C}_1}{15}=\dfrac{2}{15}$
以上より, 求める期待値は,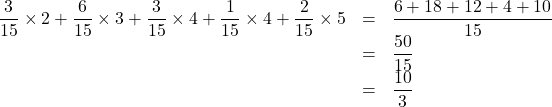
$\begin{array}{lll}\dfrac{3}{15}\times2+\dfrac{6}{15}\times3+\dfrac{3}{15}\times4+\dfrac{1}{15}\times4+\dfrac{2}{15}\times5&=&\dfrac{6+18+12+4+10}{15}\\&=&\dfrac{50}{15}\\&=&\dfrac{10}{3}\end{array}$
$\dfrac{10}{3}\cdots$ (答)

佐賀大学

解答・解説

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル