こんにちは。よくある問題ですね。典型問題なので落としたくないですね。それではどうぞ。
【問題】公園の空き地に正方形の形をした花だんをつくる予定である。下の図のように, その花だんの中に, 幅3mの通路をつくると, 花を植える部分の面積の合計は60m![]() になる。次の(1)・(2)に答えなさい。
になる。次の(1)・(2)に答えなさい。
(1) 次の![]() に答えなさい。
に答えなさい。![]() この正方形の花だんの1辺の長さを
この正方形の花だんの1辺の長さを![]() とすると, 通路の面積を
とすると, 通路の面積を![]() を用いた式で表しなさい。
を用いた式で表しなさい。![]() この正方形の花だんの1辺の長さを求めなさい。
この正方形の花だんの1辺の長さを求めなさい。
(2) 当初予定していた花だんより広くつくることに変更した。下の図のように, 花だんの形は変わらず正方形とし, その花だんの中には, 幅2mの通路をつくることにした。このようにすると, 花を植える部分の面積の合計は![]() になる。このとき, この正方形の花だんの1辺の長さを求めなさい。
になる。このとき, この正方形の花だんの1辺の長さを求めなさい。
【2023年徳島県第2回基礎学力テスト】
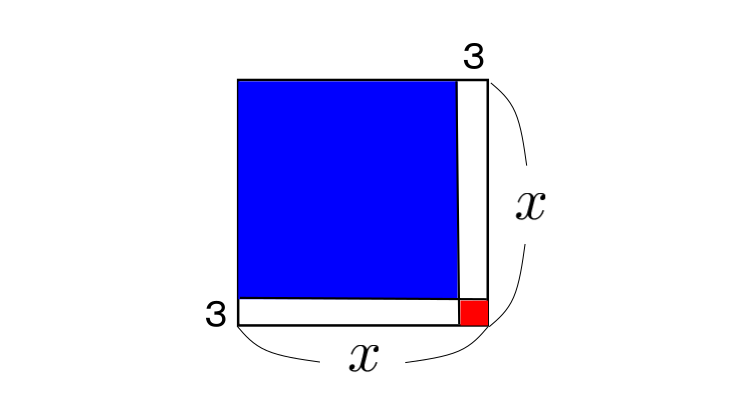
(1) ![]() この手の問題は通路をずらして考えると考えやすくなる。
この手の問題は通路をずらして考えると考えやすくなる。
以下の図のように通路を右と下に寄せる。
通路は長方形の形をしており, 縦横は3m, ![]() mである。それが2つあるので面積の合計は
mである。それが2つあるので面積の合計は![]() となるが, 図の赤い1辺3mの正方形の部分は2つの長方形の重なり部分であるため
となるが, 図の赤い1辺3mの正方形の部分は2つの長方形の重なり部分であるため![]() から1回引かなくてはならない。よって, 求める面積は,
から1回引かなくてはならない。よって, 求める面積は, ![]() (答)
(答)![]()
上の青色の部分は正方形で, 1辺は![]() である。その面積が
である。その面積が![]() なので,
なので, ![]() という方程式ができる。
という方程式ができる。
これを解くと, ![]() となるが, 1辺は通路の幅より長くなくてはならないので,
となるが, 1辺は通路の幅より長くなくてはならないので, ![]() は不適。
は不適。
よって, 花だんの1辺の長さは, ![]()
(2)
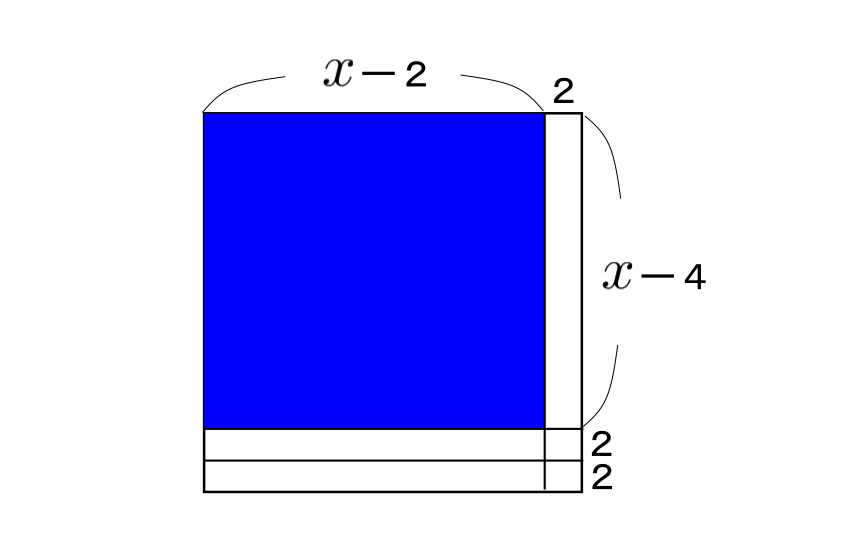
これも(1)と同様に通路を右と下に寄せると, 下図のようになる。ただし, 花だんの1辺は![]() とする。
とする。
青色の部分は長方形でその面積が![]() なので,
なので, ![]()
![]()
![]()
![]() より,
より, ![]()
![]() (答)
(答)
 数樂管理人のブログ
数樂管理人のブログ