こんにちは。これもしっかりと得点源にしたいパターンが目白押しの問題ですね。
問題
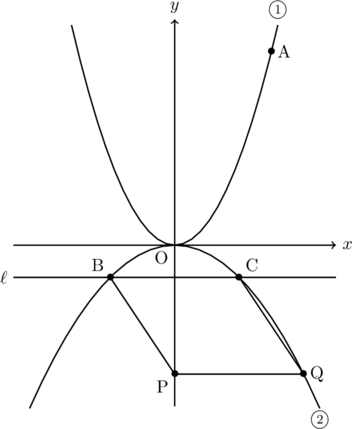
下の図で, グラフ は関数
は関数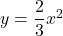 のグラフで, グラフ
のグラフで, グラフ は関数
は関数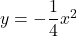 のグラフである。グラフ
のグラフである。グラフ 上に
上に 座標が3である点Aをとる。直線
座標が3である点Aをとる。直線 の式は
の式は である。グラフ
である。グラフ と直線
と直線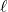 との交点をそれぞれB, Cとする。Bの
との交点をそれぞれB, Cとする。Bの 座標は負, Cの
座標は負, Cの 座標は正である。また,
座標は正である。また, 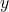 軸上に点P
軸上に点P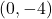 をとり, Pを通り,
をとり, Pを通り,  軸に平行な直線と関数
軸に平行な直線と関数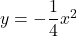 との交点をQとする。Qの
との交点をQとする。Qの 座標は正とする。次の(1)~(4)に答えなさい。
座標は正とする。次の(1)~(4)に答えなさい。
(1) 点Aの座標を求めなさい。
(2) 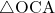 の面積を求めなさい。
の面積を求めなさい。
(3) 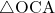 の面積と四角形BPQCの面積の比を最もかんたんな整数の比で表しなさい。
の面積と四角形BPQCの面積の比を最もかんたんな整数の比で表しなさい。
(4) 次の に答えなさい。
に答えなさい。
 点Bを通り, 四角形BPQCの面積を二等分する直線の式を求めなさい。
点Bを通り, 四角形BPQCの面積を二等分する直線の式を求めなさい。

 軸上に, 点
軸上に, 点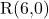 をとり, Rを通る直線が四角形BPQCの面積を二等分するとき, この直線の式を求めなさい。
をとり, Rを通る直線が四角形BPQCの面積を二等分するとき, この直線の式を求めなさい。
【2023年徳島県第2回基礎学力テスト】解答・解説
(1) 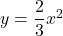 に
に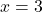 を代入して,
を代入して, 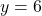
よって,
A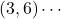 (答)
(答)
(2) B, Cの座標を求める。
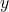 座標が
座標が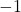 であるから,
であるから, 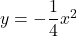 で
で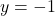 とすると,
とすると,
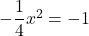
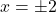 となり, B
となり, B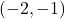 , C
, C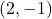 となる。
となる。
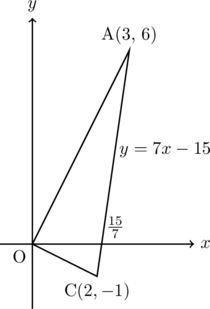
 の面積は点A, Cから
の面積は点A, Cから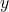 軸に垂線をひき, 台形を作って余分な三角形を引けば求まるが, ここでは直線ACを求めてやってみようと思う。
軸に垂線をひき, 台形を作って余分な三角形を引けば求まるが, ここでは直線ACを求めてやってみようと思う。
直線ACは2点A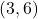 , C
, C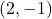 を通るので, その式は,
を通るので, その式は, 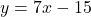 となり, この直線と
となり, この直線と 軸との交点は,
軸との交点は, 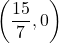 である。また点Aと点Cの
である。また点Aと点Cの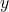 軸方向だけ見た場合の距離(高さ)は
軸方向だけ見た場合の距離(高さ)は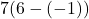 である。したがって, 求める面積は,
である。したがって, 求める面積は,
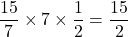
 (答)
(答)
(3) P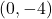 より, Qの座標を求める。
より, Qの座標を求める。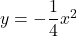 で
で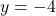 として,
として, 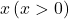 を求めると,
を求めると, 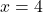
したがって, Q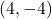 である。これより,
である。これより, 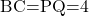 ,
, 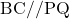 であるから, 四角形BPQCは平行四辺形である。この平行四辺形は底辺が4, 高さが3なので, 面積は
であるから, 四角形BPQCは平行四辺形である。この平行四辺形は底辺が4, 高さが3なので, 面積は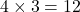 。よって求める面積比は,
。よって求める面積比は,
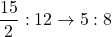
 (答)
(答)
(4)
 とも平行四辺形の面積を二等分する直線の式を求める問題である。平行四辺形の面積を二等分する直線は, 必ずと言っていいほど, 対角線の中点を通る。今回もそれである。
とも平行四辺形の面積を二等分する直線の式を求める問題である。平行四辺形の面積を二等分する直線は, 必ずと言っていいほど, 対角線の中点を通る。今回もそれである。 に関して言えば2点B, Qを通る直線でも求められるが, 結局対角線の中点を通っているので, 今回は
に関して言えば2点B, Qを通る直線でも求められるが, 結局対角線の中点を通っているので, 今回は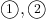 ともに対角線の中点を求めてから, 問題を解いていこうと思う。
ともに対角線の中点を求めてから, 問題を解いていこうと思う。
 対角線の中点の座標は, C
対角線の中点の座標は, C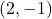 , P
, P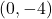 であるから,
であるから,
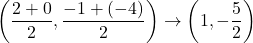
よって, 求める直線の式は, 2点B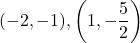 を通る直線である。
を通る直線である。
したがって, 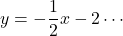 (答)
(答)
 求める直線の式は, 2点
求める直線の式は, 2点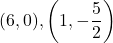 を通る直線である。
を通る直線である。
したがって, 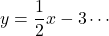 (答)
(答)
【補足】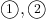 とも座標が分数を含むとき, 直線の式を求めるのは,
とも座標が分数を含むとき, 直線の式を求めるのは, 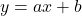 に通る2点の座標を代入して連立方程式を解いて求めるといいでしょう。
に通る2点の座標を代入して連立方程式を解いて求めるといいでしょう。 ![]() は関数
は関数![]() のグラフで, グラフ
のグラフで, グラフ![]() は関数
は関数![]() のグラフである。グラフ
のグラフである。グラフ![]() 上に
上に![]() 座標が3である点Aをとる。直線
座標が3である点Aをとる。直線![]() の式は
の式は![]() である。グラフ
である。グラフ![]() と直線
と直線![]() との交点をそれぞれB, Cとする。Bの
との交点をそれぞれB, Cとする。Bの![]() 座標は負, Cの
座標は負, Cの![]() 座標は正である。また,
座標は正である。また, ![]() 軸上に点P
軸上に点P![]() をとり, Pを通り,
をとり, Pを通り, ![]() 軸に平行な直線と関数
軸に平行な直線と関数![]() との交点をQとする。Qの
との交点をQとする。Qの![]() 座標は正とする。次の(1)~(4)に答えなさい。
座標は正とする。次の(1)~(4)に答えなさい。
![]() に
に![]() を代入して,
を代入して, ![]()
![]() (答)
(答)![]() 座標が
座標が![]() であるから,
であるから, ![]() で
で![]() とすると,
とすると, ![]()
![]() となり, B
となり, B![]() , C
, C![]() となる。
となる。
 数樂管理人のブログ
数樂管理人のブログ 


