こんにちは。空間ベクトルのなす角のちょっとした応用?問題です。それではいってみましょう。
【問題】大きさ4の![]() が,
が, ![]() 軸の正の向きとなす角が
軸の正の向きとなす角が![]() で,
で, ![]() 軸の正の向きとなす角が
軸の正の向きとなす角が![]() のとき,
のとき, ![]() の成分を求めよ。また,
の成分を求めよ。また, ![]() が
が![]() 軸の正の向きとなす角の大きさを求めよ。
軸の正の向きとなす角の大きさを求めよ。
【解答・解説】以下のイメージを参照してください。

これから![]() 座標は
座標は![]() ,
, ![]() 座標は
座標は![]() となる。これより,
となる。これより, ![]() とおくと,
とおくと, ![]() より,
より, ![]()
![]()
![]()
![]() 軸の正の向きの単位ベクトルを
軸の正の向きの単位ベクトルを![]() とする。
とする。![]()
![]() のとき,
のとき, ![]() より,
より, ![]() と
と![]() 軸のなす角を
軸のなす角を![]() とすると,
とすると, 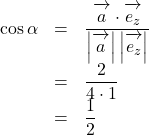
![]() より,
より, ![]()
![]()
![]() のとき,
のとき, ![]() より,
より, ![]() と
と![]() 軸のなす角を
軸のなす角を![]() とすると,
とすると, 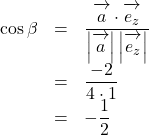
![]() より,
より, ![]()
以上より, ![]() は
は![]() のとき,
のとき, ![]() 軸の正の向きとなす角は
軸の正の向きとなす角は![]() ,
, ![]() のときは,
のときは, ![]() 軸の正の向きとなす角は
軸の正の向きとなす角は![]() である。
である。
 数樂管理人のブログ
数樂管理人のブログ 


