高校数学：確率：条件付き確率(岐阜薬科大学)

2023年12月6日

こんにちは。頻出系ですかね。早速やってみましょう。

岐阜薬科大学の問題

【問題】ある病気にかかっている人が $4\%$ いる集団Aがある。病気 $X$ を診断する検査で, 病気 $X$ にかかっている人が正しく陽性と判断される確率は $80\%$ である。また, この検査で病気 $X$ にかかっていない人が誤って陽性と判断される確率は $10\%$ である。
(1) 集団Aのある人がこの検査を受けたところ陽性と判断された。この人が病気 $X$ にかかっている確率はいくらか。
(2) 集団Aのある人がこの検査を受けたところ陰性と判断された。この人が実際には病気 $X$ にかかっている確率はいくらか。
【岐阜薬科大】

解答・解説

条件を整理すると下図のようになる。

(1) 求める確率は

で求められるので,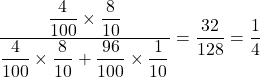
$\dfrac{\dfrac{4}{100}\times\dfrac{8}{10}}{\dfrac{4}{100}\times\dfrac{8}{10}+\dfrac{96}{100}\times\dfrac{1}{10}}=\dfrac{32}{128}=\dfrac14$
$\dfrac{1}{4}\cdots$ (答)
(2) 求める確率は

で求められるので,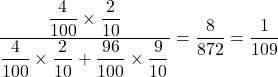
$\dfrac{\dfrac{4}{100}\times\dfrac{2}{10}}{\dfrac{4}{100}\times\dfrac{2}{10}+\dfrac{96}{100}\times\dfrac{9}{10}}=\dfrac{8}{872}=\dfrac{1}{109}$
$\dfrac{1}{109}\cdots$ (答)

岐阜薬科大学の問題

解答・解説

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル