こんにちは。知っておくと便利な合同式。その性質と証明と使い方を書いておきます。早速やっていきましょう。
ある整数![]() を整数
を整数![]() を割ったときの余りが等しいとき,
を割ったときの余りが等しいとき, ![]() と
と![]() は
は![]() を法として合同(
を法として合同(![]() で割った余りが等しい)と言います。
で割った余りが等しい)と言います。
例えば, 14と8を6で割ったときの余りはともに2ですから, 14と8は6を法として合同(6で割った余りが等しい)と言います。
これを数学の記号では, ![]()
読み方は
「14合同8モッド6」と読みます。
と書きます。![]() ~とは~で割った余りということです。
~とは~で割った余りということです。
他に7と10は3で割ると余りがともに1なので, ![]() となります。
となります。
![]() ,
, ![]() ならば,
ならば, ![]() 和
和 ![]()
![]() 差
差 ![]()
![]() 積
積 ![]()
![]() 商
商 ![]()
![]() と
と![]() は互いに素ならば,
は互いに素ならば, ![]()
![]() 累乗
累乗 ![]()
![]() は自然数
は自然数
が言えます。
以下![]() を法として話を進めていきます。特に断りのない場合はすべて
を法として話を進めていきます。特に断りのない場合はすべて![]() です。
です。
また, ![]() なので,
なので, ![]() ,
, ![]() とし,
とし, ![]() なので,
なので, ![]() ,
, ![]() とする。
とする。
ただし, ![]() は整数とする。
は整数とする。
![]() の証明
の証明![]()
![]()
以上より, ![]() で割った余りが等しいので,
で割った余りが等しいので, ![]()
![]() の証明
の証明![]()
![]()
以上より, ![]() で割った余りが等しいので,
で割った余りが等しいので, ![]()
![]() の証明
の証明![]()
![]()
以上より, ![]() で割った余りが等しいので,
で割った余りが等しいので, ![]()
![]()
![]() と
と![]() は互いに素ならば,
は互いに素ならば, ![]() の証明
の証明![]() なので,
なので, ![]() より,
より, ![]() は
は![]() の倍数。
の倍数。
また, ![]() と
と![]() は互いに素なので,
は互いに素なので, ![]() が
が![]() の倍数である。
の倍数である。
よって, ![]()
つまり, ![]()
互いに素でなければ,
例えば, ![]() の辺々を2で割ると,
の辺々を2で割ると, ![]() となり合同が成り立ちません。
となり合同が成り立ちません。
互いに素であるなら,
例えば, ![]() の辺々を2で割っても,
の辺々を2で割っても, ![]() となり合同が成り立ちます。
となり合同が成り立ちます。
![]() の証明
の証明
二項定理を用いて展開していきます。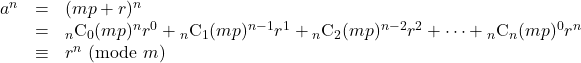
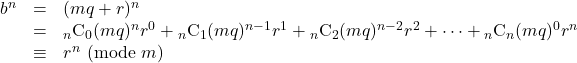
以上より, ![]() で割った余りが等しいので,
で割った余りが等しいので, ![]()
【例】![]() は6で割って4余る整数です。このとき,
は6で割って4余る整数です。このとき, ![]() を6で割った余りを求めなさい。
を6で割った余りを求めなさい。
合同式を用いない場合は, ![]() とおいて代入していって計算していくのがお決まりである。
とおいて代入していって計算していくのがお決まりである。
今回はそうではなく, 余りに着目して解くとどうなるかということである。![]() を6で割った余りが4なので
を6で割った余りが4なので![]()
合同式は累乗できるので, ![]() の辺々2乗して
の辺々2乗して![]()
合同式は掛け算できるので, ![]() の辺々5倍(
の辺々5倍(![]() を掛ける)して,
を掛ける)して, ![]()
![]()
![]() とすると,
とすると, ![]()
したがって, 求める余りは3
【例】![]() を13で割った余りを求めよ。
を13で割った余りを求めよ。
![]() でこのとき, 13で割ると余りが
でこのとき, 13で割ると余りが![]() になります。これを使うと次のようになります。
になります。これを使うと次のようになります。![]()
求めるのは100乗なので, 辺々33乗して4をかけると, ![]()
![]()
よって, 求める余りは9
※余り![]() ということは, 余り9と合同
ということは, 余り9と合同
 なんで7の100乗を6で割った余りが1なの?
なんで7の100乗を6で割った余りが1なの?
 高校数学:合同式を用いた一次不定方程式の解法
高校数学:合同式を用いた一次不定方程式の解法
 高校数学:整数:整数問題・余り①(合同式の考え方を用いて)
高校数学:整数:整数問題・余り①(合同式の考え方を用いて)
 数樂管理人のブログ
数樂管理人のブログ 
