こんにちは。たまに参考書とかに載っている, ![]() として,
として, ![]() ,
, ![]() ,
, ![]() を置換する方法を書いておきます。
を置換する方法を書いておきます。
まず準備する公式たちを紹介します。
準備する公式たち
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
結論として, ![]() とおくと,
とおくと, ![]() などがどうなるか示しておきます。
などがどうなるか示しておきます。
tan(x/2)=tとすると
![]()
![]()
![]()
![]()
![]()
![]()
以下, これらの詳細を書き, 最後にこれらを使って例題を解いてみましょう。
![]() とおいて,
とおいて, ![]() を
を![]() を用いて表せ。
を用いて表せ。
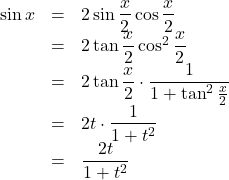
よって, ![]()
![]() とおいて,
とおいて, ![]() を
を![]() を用いて表せ。
を用いて表せ。
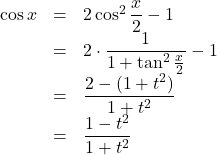
よって, ![]()
【別解】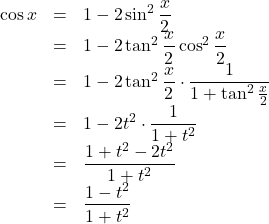
よって, ![]()
![]() から
から![]() を示せ。
を示せ。
![]() とし,
とし, ![]() で微分すると,
で微分すると, 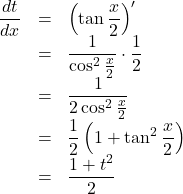
よって, ![]()
したがって, ![]()
【例】![]() を
を![]() として求めよ。
として求めよ。
![]() とおくと,
とおくと, ![]() ,
, ![]() なので,
なので, 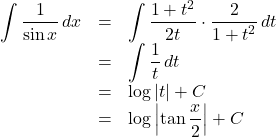
よって, ![]() (
(![]() は積分定数)
は積分定数)
【例】![]() を
を![]() として求めよ。
として求めよ。
![]() とおくと,
とおくと, ![]() ,
, ![]() ,
, ![]() なので,
なので, 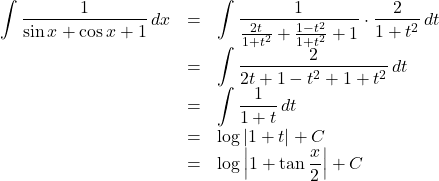
よって, ![]() (
(![]() は積分定数)
は積分定数)
 数樂管理人のブログ
数樂管理人のブログ 
