こんにちは。積分漸化式の攻略のカギは部分積分です。早速いってみましょう。
【例】![]() について,
について, ![]() と
と![]() の関係を示せ。
の関係を示せ。
【解答例】![]() とする。
とする。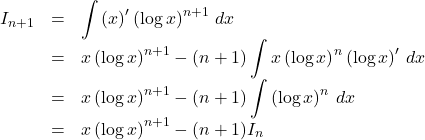
よって, ![]()
【例】![]() について,
について, ![]() と
と![]() の関係を示せ。
の関係を示せ。
【解答例】![]() とする。
とする。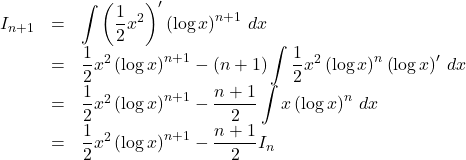
よって, ![]()
 高校数学:数III積分:sinⁿx, cosⁿx, tanⁿxの積分漸化式
高校数学:数III積分:sinⁿx, cosⁿx, tanⁿxの積分漸化式  高校数学:数III積分:xⁿe^x系の積分漸化式
高校数学:数III積分:xⁿe^x系の積分漸化式こんにちは。積分漸化式の攻略のカギは部分積分です。早速いってみましょう。
【例】![]() について,
について, ![]() と
と![]() の関係を示せ。
の関係を示せ。
【解答例】![]() とする。
とする。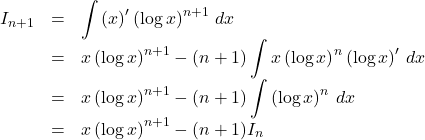
よって, ![]()
【例】![]() について,
について, ![]() と
と![]() の関係を示せ。
の関係を示せ。
【解答例】![]() とする。
とする。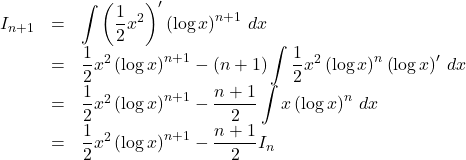
よって, ![]()
 高校数学:数III積分:sinⁿx, cosⁿx, tanⁿxの積分漸化式
高校数学:数III積分:sinⁿx, cosⁿx, tanⁿxの積分漸化式  高校数学:数III積分:xⁿe^x系の積分漸化式
高校数学:数III積分:xⁿe^x系の積分漸化式