こんにちは。![]() 系の頻出系の漸化式を書いていきます。基本的に積分漸化式は部分積分を用いて攻略していきます。
系の頻出系の漸化式を書いていきます。基本的に積分漸化式は部分積分を用いて攻略していきます。
【例】![]() について,
について, ![]() と
と![]() の関係を示せ。
の関係を示せ。
【解答例】![]() として部分積分していく。
として部分積分していく。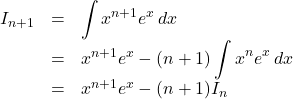
よって, ![]()
出題の傾向としては積分区間が0~1で出題されることが多いです。
【例】![]() が
が![]() となることを示せ。
となることを示せ。
【解答例】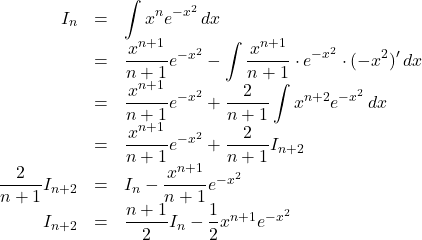
よって, ![]()
出題の傾向としては積分区間が0~1で出題されることが多いです。
 高校数学:数III積分:sinⁿx, cosⁿx, tanⁿxの積分漸化式
高校数学:数III積分:sinⁿx, cosⁿx, tanⁿxの積分漸化式  高校数学:数III積分:(logx)ⁿ系の積分漸化式
高校数学:数III積分:(logx)ⁿ系の積分漸化式 数樂管理人のブログ
数樂管理人のブログ 
