TikZ：中学数学：平面図形：面積比の問題(和歌山県)

こんにちは。面積比の問題です。

和歌山県一部抜粋

【問題】図のように, $\text{AB}=4\, \text{cm}$ , $\text{BE}=3\, \text{cm}$ , $\text{EC}=2\, \text{cm}$ のとき, 辺BAの延長上に $\text{AG}=2\, \text{cm}$ となるように点Gをとる。また, GEとADの交点をHとする。
このとき, 台形ABEHの面積は, 平行四辺形ABCDの面積の何倍になるか, 求めなさい。

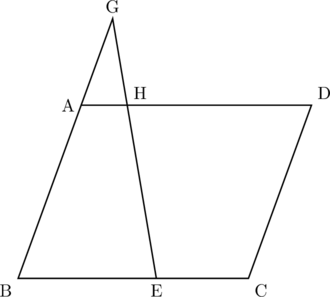
【和歌山県一部抜粋】

解答・解説

【解答】 $\dfrac{2}{5}$ 倍
【解説】

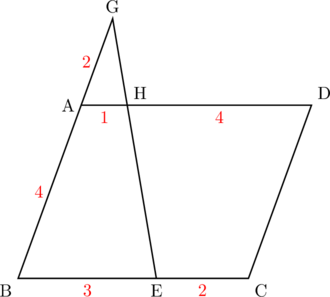
高さが等しい台形と平行四辺形の面積比は,
台形の(上底＋下底)：(平行四辺形の底辺) $\times2\cdots\maru1$
で求められる。平行四辺形の底辺は $5\, \text{cm}$ と分かっていて, 台形の下底は $3\,\text{cm}$ と分かっているので, 必要なのは台形の上底である $\text{AH}$ の長さだけ分かればよい。
$\bigtriangleup{\text{GAH}}$ ∽ $\bigtriangleup{\text{GBE}}$ で, 相似比は $\text{GA} : \text{GB} = 1 : 3$ であるから,
$1 : 3 = \text{AH} : 3$ より, $\text{AH}=1\, \text{cm}$
よって, 台形ABEHの上底と下底の和は $1+3=4$ , 平行四辺形の底辺の2倍は $5\times2=10$
ゆえに求める答えは,
$4\div10=\dfrac25$
$\dfrac25$ 倍 $\cdots$ (答)
※【補足】 $\maru1$ の考え方ができるのは, 平行四辺形を上底と下底が等しい台形とみなしているからです。これを用いれば高さの等しい長方形や正方形でも同じ考え方ができます。

和歌山県一部抜粋

解答・解説

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル