こんにちは。令和6年1月10日に実施されたものです。設定自体は平易だと思います。早速やってみましょう。
【問題】まおさんは, 家を午前10時に出発し, 歩いて図書館に行った。図書館にしばらくいた後, 図書館を出て, 途中のケーキ屋で買い物をして帰宅した。図1は, まおさんが歩いているときの速さは分速75mで一定とし, 家を出てから![]() 分後に, 家から
分後に, 家から![]() mの地点にいるとして,
mの地点にいるとして, ![]() と
と![]() の関係をグラフに表したものである。
の関係をグラフに表したものである。
次の(1)~(3)に答えなさい。
図1
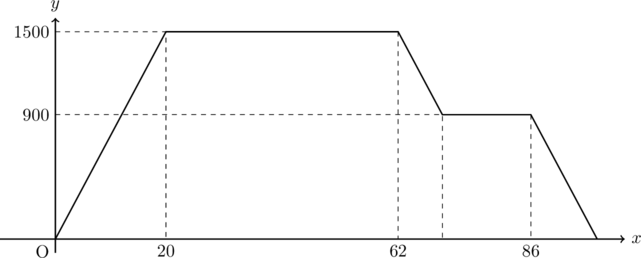
(1) 次のア~ウにあてはまる数を答えなさい。また, エにあてはまる時刻は何時何分か答えなさい。
・まおさんは図書館に【ア】分間滞在した。
・まおさんは図書館を出て, ケーキ屋まで【イ】分間歩いた。
・まおさんはケーキ屋に【ウ】分間滞在した。
・まおさんが帰宅したのは【エ】である。
(2) まおさんが図書館を出て, ケーキ屋に着くまでの様子を表す部分のグラフについて,
(3) まおさんの姉は, 午前10時50分にまおさんの家を出発し, 分速85mの速さで歩いて図書館に向かった。すると, 図書館からケーキ屋に向かっているまおさんと出会った。2人が出会った時刻は何時何分か。また, 家から何mの地点で出会ったか求めなさい。ただし, まおさんの姉の歩く速さは一定であるとする。
【R5徳島県第3回基礎学力テスト】
【解答解説】
(1)
・滞在したのは![]() 分間。
分間。![]() ア
ア
・図書館とケーキ屋の距離は![]() , それを分速75mで歩いたので,
, それを分速75mで歩いたので, ![]() 分間歩いた。
分間歩いた。![]() イ
イ
・イよりケーキ屋に着いたのは出発してから![]() 分後。
分後。
よって, 滞在したのは![]() 分間。
分間。![]() ウ
ウ
・![]() なので家に帰ってきたのは, 出発してから
なので家に帰ってきたのは, 出発してから![]() 分後。
分後。
午前![]() 時
時![]() 分
分![]() 午前11時38分
午前11時38分![]() エ
エ
(2)
求める直線の式は下の図の直線ABである。
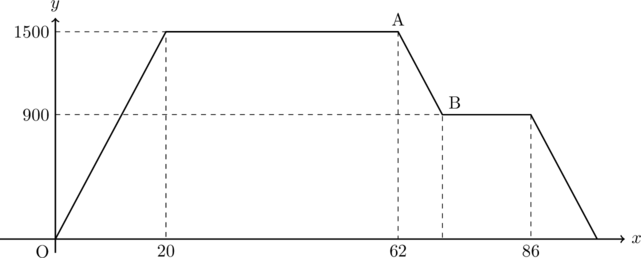
1分あたりに75m進み, 右下がりの直線なので, 傾きは
よって, 求める直線は,
(3)
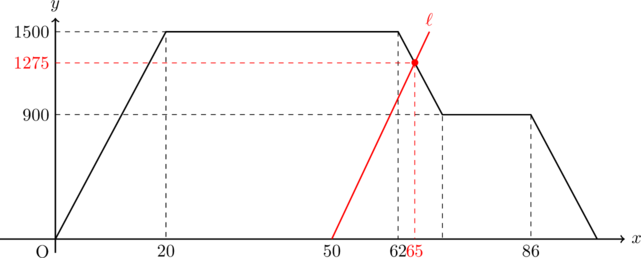
上の図の直線
これと(2)で求めた
午前
よって,
出会った時刻は, 午前11時5分
家から
【別解(略解)】(3)は式を求めるのが面倒なら, 算数でやっても求められる。
 数樂管理人のブログ
数樂管理人のブログ 


